 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема2:. Графический метод решения задач линейного программирования
Задание 1
Решить графическим методом:
1) 
при 
РЕШЕНИЕ
L1: L2: L3:
| L1: | A | B | L2: | A | B | L3: | A | B | ||
| x1 | x1 | x1 | ||||||||
| x2 | x2 | x2 |
Решение находится, исходя из решения системы:
Тогда:  =_______;
=_______;  =_________ и min Z=
=_________ и min Z=
Ответ:
2) 
при
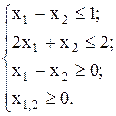
РЕШЕНИЕ
L1: L2: L3:
| L1: | A | B | L2: | A | B | L3: | A | B | ||
| x1 | x1 | x1 | ||||||||
| x2 | x2 | x2 |
Решение находится, исходя из решения системы:
Тогда:  =_______;
=_______;  =_________ и max Z=
=_________ и max Z=
Ответ:
3) 
при

РЕШЕНИЕ
L1: L2:
| L1: | A | B | L2: | A | B | |
| x1 | x1 | |||||
| x2 | x2 |
Решение находится, исходя из решения системы:
Тогда:  =_______;
=_______;  =_________ и max Z=
=_________ и max Z=
Ответ:
4) 
при

РЕШЕНИЕ
L1: L2: L3:
| L1: | A | B | L2: | A | B | L3: | A | B | ||
| x1 | x1 | x1 | ||||||||
| x2 | x2 | x2 |
Решение находится, исходя из решения системы:
Тогда:  =_______;
=_______;  =_________ и min Z=
=_________ и min Z=
Ответ:
5) 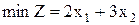
при 
РЕШЕНИЕ
L1: L2:
| L1: | A | B | L2: | A | B | |||||
| x1 | x1 | |||||||||
| x2 | x2 |
Решение находится, исходя из решения системы:
Тогда:  =_______;
=_______;  =_________ и min Z=
=_________ и min Z=
Ответ:
Задание 2
Решить графически:
1) 
при

РЕШЕНИЕ
Преобразуем данную систему к системе неравенств с двумя переменными
Тогда ЗЛП примет вид:
Целевая функция:
________________________________________
Система ограничений:
L1: L2: L3:
| L1: | A | B | L2: | A | B | L3: | A | B | ||
| x1 | x1 | x1 | ||||||||
| x2 | x2 | x2 |
L4:
| L4: | A | B | ||||||||
| x1 | ||||||||||
| x2 |
Решение находится, исходя из решения системы:
Тогда:  =_____;
=_____;  =______;
=______;  =____;
=____;  =___;
=___;  =____;
=____; 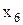 =____
=____
и max Z=
Ответ:
2) 
при 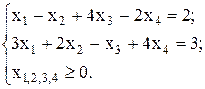
РЕШЕНИЕ
Преобразуем данную систему к системе неравенств с двумя переменными
Тогда ЗЛП примет вид:
Целевая функция:
________________________________________
Система ограничений:
L1: L2:
| L1: | A | B | L2: | A | B | |||||
| x1 | x1 | |||||||||
| x2 | x2 |
Решение находится, исходя из решения системы:
Тогда:  =_____;
=_____;  =____;
=____;  =____;
=____;  =____ и max Z=
=____ и max Z=
Ответ:
3) 
при

РЕШЕНИЕ
Преобразуем данную систему к системе неравенств с двумя переменными
Тогда ЗЛП примет вид:
Целевая функция:
________________________________________
Система ограничений:
L1: L2: L3:
| L1: | A | B | L2: | A | B | L3: | A | B | ||
| x1 | x1 | x1 | ||||||||
| x2 | x2 | x2 |
L4:
| L4: | A | B | ||||||||
| x1 | ||||||||||
| x2 |
Решение находится, исходя из решения системы:
Тогда:  =_____;
=_____;  =______;
=______;  =____;
=____;  =___;
=___;  =____;
=____;  =_____
=_____
и min Z=
Ответ:
Задание 3
1) На мебельной фабрике из стандартных листов фанеры необходимо вырезать заготовки трех видов в количествах соответственно равных 24, 31 и 18 шт. Каждый лист фанеры может быть разрезан на заготовки двумя способами. Количество получаемых заготовок при данном способе раскроя приведено в таблице. В ней же указана величина отходов, которые получаются при данном способе Раскроя одного листа фанеры.
Определить, сколько листов фанеры и по какому способу нужно раскроить так, чтобы было получено не меньше нужного количества заготовок при минимальных отходах.
| Способ раскроя Вид заготовки | Количество заготовок | |
| I II III | ||
| Величина отходов: |
РЕШЕНИЕ
Составим математическую модель задачи:
Целевая функция:
Система ограничений:
L1: L2: L3:
| L1: | A | B | L2: | A | B | L3: | A | B | ||
| x1 | x1 | x1 | ||||||||
| x2 | x2 | x2 |
Поиск по сайту: