 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема 1: Линейное программирование. Графическая интерпретация задачи линейного программирования
Федеральное агентство по образованию
ГОУ ВПО "Шадринский государственный педагогический институт"
Артемова С.В.
Слинкина И.Н.
Исследование операций
Рабочая тетрадь № 2
Шадринск
УДК 681.3 (075.8)
ББК 32.973 26я 73
С 476
Артемова С.В., Слинкина И.Н.
Исследование операций: Рабочая тетрадь. Учебно-методическое пособие. – Шадринск: изд-во Шадринского государственного педагогического института, 2008. - 120 с.
Слинкина И.Н. – кандидат педагогических наук, доцент кафедры прикладной математики
Артемова С.В. – старший преподаватель кафедры прикладной математики
Рецензенты: к.п.н., доцент кафедры ПМ Оболдина Т.А.
к.п.н., доцент кафедры ПСТ Коуров А.В.
Рабочая тетрадь по курсу «Исследование операций предназначена для студентов третьего курса факультетов информатики и физико-математического, первой или второй специальностью которых является «Информатика». В данном учебно-методическом пособии представлены задачи и упражнения по темам «Линейное программирование», «Нелинейное программирование», «Теория игр» и «Теория массового обслуживания».
© Шадринский государственный педагогический институт
©Артемова С.В., Слинкина И.Н., 2008
ОГЛАВЛЕНИЕ
Вопросы к блокам.. 4
Тема 1: Линейное программирование. Графическая интерпретация задачи линейного программирования. 6
Тема2:. Графический метод решения задач линейного программирования 13
Самостоятельная работа № 1. 26
Тема 3: Симплексный метод решения задач линейного программирования 28
Самостоятельная работа № 2. 42
Тема 4: Двойственные задачи. 45
Самостоятельная работа №3. 56
Тема 5: Транспортные задачи. 59
Самостоятельная работа № 4. 67
Тема 6: Транспортные задачи с ограничениями по пропускной способности 68
Тема 7: Нелинейное программирование. 75
Самостоятельная работа № 5. 85
Тема 8: Теория игр. 86
Тема 9. Теория массового обслуживания. 97
Лабораторное занятие № 1. 105
Лабораторное занятие №2. 109
Домашняя контрольная работа. 110
Вопросы к блокам
Блок 1
1. Предмет и задачи исследования операций.
2. Основные понятия и принципы исследования операций.
3. Математические модели операций.
4. Понятие линейного программирования.
5. Примеры экономических задач линейного программирования. Задача о наилучшем использовании ресурсов.
6. Примеры экономических задач линейного программирования. Задача о выборе оптимальных технологий.
7. Примеры экономических задач линейного программирования. Задача о смесях.
8. Примеры экономических задач линейного программирования. Транспортная задача.
9. Основные виды записи задач линейного программирования.
10. Способы преобразования.
11. Переход к канонической форме.
12. Переход к симметричной форме записи.
Блок 2
1. Геометрическая интерпретация задачи линейного программирования.
2. Решение задач линейного программирования графическим методом.
3. Свойства решений задачи линейного программирования.
4. Общая идея симплексного метода.
5. Построение начального опорного плана при решении задач линейного программирования симплексным методом.
6. Признак оптимальности опорного плана. Симплексные таблицы.
7. Переход к нехудшему опорному плану.
8. Симплексные преобразования.
9. Альтернативный оптимум (признак бесконечности множества опорных планов).
10. Признак неограниченности целевой функции.
11. Понятие о вырождении. Монотонность и конечность симплексного метода. Зацикливание.
12. Понятие двойственности для симметричных задач линейного программирования.
Блок 3
1. Несимметричные двойственные задачи.
2. Открытая и закрытая модели транспортной задачи.
3. Построение начального опорного плана. Правило "Северо-западного угла".
4. Построение начального опорного плана. Правило минимального элемент.
5. Построение начального опорного плана. Метод Фогеля.
6. Метод потенциалов.
7. Решение транспортных задач с ограничениями по пропускной способности.
8. Примеры задач дискретного программирования. Задача о контейнерных перевозках. Задача о назначении.
9. Сущность методов дискретной оптимизации.
10. Задача выпуклого программирования.
11. Метод множителей Лагранжа.
12. Градиентные методы.
Блок 4
1. Метод штрафных и барьерных функций.
2. Динамическое программирование. Основные понятия. Сущность методов решения.
3. Стохастические программирование. Основные понятия.
4. Матричные игры с нулевой суммой.
5. Чистые и смешанные стратегии и их свойства.
6. Задачи теории массового обслуживания. Классификация систем массового обслуживания.
7. Схема гибели и размножения. Формула Литтла.
8. Простейшие системы массового обслуживания и их характеристики.
9. Потоки событий.
Тема 1: Линейное программирование. Графическая интерпретация задачи линейного программирования
Задание 1
Составить математическую модель задачи:
а) Для изготовления трех видов изделий А, В и С используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования указаны в таблице. В ней же указан общий фонд рабочего времени каждого из типов используемого оборудования, а также прибыль от реализации одного изделия каждого вида.
Требуется определить, сколько изделий и какого вида следует изготовить предприятию, чтобы прибыль от их реализации была максимальной.
| Тип оборудования | Затраты времени (станко-ч) на обработку одного изделия вида | Общий фонд рабочего времени оборудования (ч) | ||
| А | В | С | ||
| Фрезерное Токарное Сварочное Шлифовальное | ||||
| Прибыль (руб.) |
РЕШЕНИЕ:
Целевая функция:
_____________________________________________________
Система ограничений:
б) Продукцией городского молочного завода является молоко, кефир, сметана, расфасованная в тару ELOPAK-FASTIV. На производство 1 т молока, кефира и сметаны требуется соответственно 1010, 1010 и 9450 кг молока. При этом затраты рабочего времени при разливе 1 т молока и кефира составляют 0,18 и 0,19 машино-ч. На расфасовке 1 т сметаны заняты специальные автоматы в течение 3,25 ч. Всего для производства цельномолочной продукции завод может использовать 136000 кг молока. Основное оборудование может быть использовано 21,4 машино-ч, а автоматы для расфасовки сметаны – 16,25 ч. Прибыль от реализации 1 т молока, кефира и сметаны соответственно 3000, 2200 и 13600 руб. Завод должен ежедневно производить не менее 100 т молока. На производство другой продукции нет ограничений.
Требуется определить, какую продукцию и в каком количестве следует ежедневно изготовлять заводу, чтобы прибыль от ее реализации была максимальной.
РЕШЕНИЕ
Целевая функция:
____________________________________________
Система ограничений:
в) Кондитерская фабрика для производства трех видов карамели использует три вида основного сырья: сахарный песок, патоку и фруктовое пюре. Нормы расхода сырья каждого вида на производство 1 т карамели данного вида приведены в таблице. В ней же указано общее количество сырья каждого вида, которое может быть использовано фабрикой, а также приведена прибыль от реализации 1 т карамели данного вида.
| Вид сырья | Нормы расхода сырья (т) на 1 т карамели | Общее количество сырья | ||
| А | В | С | ||
| Сахарный песок Патока Фруктовое пюре | 0,8 0,4 – | 0,5 0,4 0,1 | 0,6 0,3 0,1 | |
| Прибыль от реализации 1 т продукции (руб.) |
Найти план производства карамели, обеспечивающий максимальную прибыль от ее реализации.
РЕШЕНИЕ
Целевая функция:
______________________________________________
Система ограничений:
г) При откорме животных каждое животное ежедневно должно получить не менее 60 ед. питательного вещества А, не менее 50 ед. вещества В и не менее 12 ед. вещества С. Указанные питательные вещества содержат три вида корма. Содержание единиц питательных веществ в 1 кг каждого из видов корма приведено в следующей таблице:
| Питательные вещества | Количество единиц питательного вещества в 1 кг корма вида | ||
| I | II | III | |
| А В С |
Составить дневной рацион, обеспечивающий получение необходимого количества питательных веществ при минимальных денежных затратах, если цена 1 кг корма I вида составляет 9 коп., корма II вида – 12 кол. и корма III вида – 10 коп.
РЕШЕНИЕ
Целевая функция:
_______________________________________
Система ограничений:
Задание 3
Построить в единой системе координат прямые:
а) 3x+4y=12 б) x-y=7 в) –x+y=0 г) 5x-4y=-9
РЕШЕНИЕ
а) 3x+4y=12 б) x-y=7 в) –x+y=0 г) 5x-4y=-9
| а: | A | B | б: | A | B | в: | A | B | г: | A | B | |||
| x | x | x | x | |||||||||||
| y | y | y | y |
Задание 4
Записать уравнения прямых, изображенных в единой системе координат:
1: 3:
2: 4:
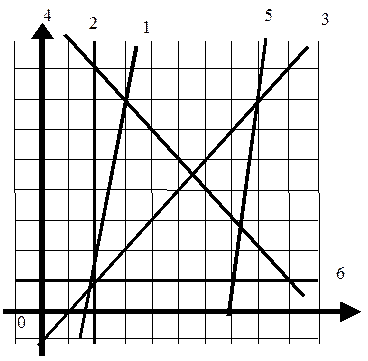
5: 6:
Задание 5
Представить графически систему линейных неравенств:
а) 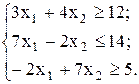 б)
б) 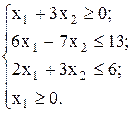
| а: | A | B | а: | A | B | б: | A | B | б: | A | B | |||
| x1 | x1 | x1 | x1 | |||||||||||
| x2 | x2 | x2 | x2 |
| а: | A | B | б: | A | B | |||||||||
| x1 | x1 | |||||||||||||
| x2 | x2 |
в)  г)
г) 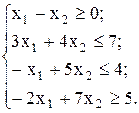
| а: | A | B | а: | A | B | б: | A | B | б: | A | B | |||
| x1 | x1 | x1 | x1 | |||||||||||
| x2 | x2 | x2 | x2 |
| а: | A | B | а: | A | B | б: | A | B | б: | A | B | |||
| x1 | x1 | x1 | x1 | |||||||||||
| x2 | x2 | x2 | x2 |
Задание 6
Записать систему неравенств, интерпретирующих данную область:
а) б)


| 1: | 1: |
| 2: | 2: |
| 3: | 3: |
| 4: | Итог:

|
| 5: | |
Итог:
|
в) г)


| 1: | 1: |
| 2: | 2: |
| 3: | 3: |
| 4: | 4: |
| 5: | |
| 6: | Итог:
|
| Итог: |
д)

| 2: | Итог:
|
Поиск по сайту: