Тема 9. Теория массового обслуживания

Задание 1

Нарисуйте граф состояний для Марковской цепи, вероятности перехода которой заданы матрицей:

Решение

Задание 2

Напишите матрицу вероятностей перехода для цепи Маркова, соответствующую графу состояний:

Решение

Задание 3

Множество состояний студентов некоторого вуза с пятилетним сроком обучения следующие: 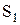- первокурсник, 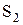- второкурсник, …, - выпускник. Студенты могут выбывать из вуза в результате его окончания или отчисления, поэтому дополним систему состояниями: - специалист, окончивший вуз, - лица, обучавшиеся в данном вузе, но не окончившие его. Составить матрицу переходов из состояния в состояние и построить граф состояний, предполагая, что исключенные не могут быть восстановлены. (Пусть р – вероятность выбыть из института, r – перейти на следующий курс, q – остаться на этом курсе).

Решение

Задание 4

Для данной системы запишите уравнения Колмогорова

Решение

Задание 5.

Погода в некотором регионе через длительные периоды времени становится то дождливой, то сухой. Если идет дождь, то с вероятностью 0,7 он будет идти на следующий день; если в какой-то день сухая погода, то с вероятностью 0,6 она сохранится и на следующий день. Известно, что в среду погода была дождливая. Какова вероятность того, что она будет дождливой в ближайшую пятницу?

Решение

Задание 6

Автомашина может находится в одном из четырех состояний: исправна; неисправна, осматривается; ремонтируется; списана. Если машина исправна, то с вероятностью 0,8 она может сломаться; если машина неисправна, то она с вероятностью 0,7 ремонтируется или с вероятностью 0,3 списывается; если же машина ремонтируется, то она с вероятностью 0,6 становится исправной, либо с вероятностью 0,4 продолжает ремонтироваться. Остальные переходы считать невозможными. Найти вероятность того, что машина будет исправна в субботу, если известно, что она была исправна в среду.

Решение.

Задание 7.

В некоторой местности климат весьма изменчив. Здесь никогда не бывает двух ясных дней подряд. Если сегодня ясно, то завтра с одинаковой вероятностью пойдет дождь или снег. Если сегодня снег (или дождь), то с вероятностью 0,5 погода не изменится. Если все же изменится, то в половине случаев снег заменяется дождем или наоборот и лишь в половине случаев на следующий день будет ясная погода. Определить вероятность хорошей погоды через три дня после дождя.

Решение.

Задание89

Предположим, что мужчин можно разделить по их профессиям на работников умственного труда, квалифицированных рабочих и неквалифицированных рабочих. Допустим, что 80% сыновей работников умственного труда становятся работниками умственного труда, 10% - квалифицированными рабочими и 10% - неквалифицированными рабочими. Пусть из сыновей квалифицированных рабочих 60% становятся квалифицированными рабочими, 20% - работниками умственного труда и 20% - неквалифицированными рабочими. Наконец, 50% сыновей неквалифицированных рабочих будут квалифицированными рабочими и по 25% пусть приходится на долю других категорий. В предположении, что каждый мужчина имеет одного сына, построить цепь Маркова с тремя состояниями, чтобы проследить за несколькими поколениями семьи. Выпишите матрицу вероятностей перехода. Найти вероятность того, что внук неквалифицированного рабочего станет работником умственного труда.

Задание 9.

В задании 9 предполагалось, что у каждого мужчины есть сын. Теперь допустим, что для мужчины вероятность иметь сына равна 0,8. Образуем Марковскую цепь с четырьмя состояниями. Первые три состояния пусть будут те же, что и в задании9, а четвертое состояние отвечает случаю, когда мужчина не имеет сына, и процесс на этом заканчивается. Это состояние представляет те семьи, в которых мужская линия вымерла. Выпишите матрицу вероятностей перехода и найдите вероятность того, что внук неквалифицированного рабочего будет работником умственного труда.

Задание 10

Прибор состоит из трех узлов; поток отказов – простейший, среднее время безотказной работы каждого узла равно =10ч. Отказавший узел сразу начинает ремонтироваться; среднее время ремонта (восстановления) узла равно =5ч; закон распределения этого времени показательный (поток восстановлений – простейший). Найти среднюю производительность прибора, если при трех работающих узлах она равна 100%, при двух – 50% а при одном и менее – прибор вообще не работает.

Решение.

Задание 11.

Прибор состоит из двух элементов: основного и резервного, работающих параллельно. Поток отказов – простейший с интенсивностью l. Отказавший элемент сразу начинают ремонтировать, среднее время ремонта . Поток восстановлений – простейший. Найти вероятность безотказной работы прибора (т.е. его надежность), если прибор работает, когда работает хотя бы один элемент, если l=0,6 и =28

Задание 12.

На телефонную линию приходят вызовы с интенсивностью 0,8 (вызовов в минуту). Средняя продолжительность разговора 1,5 мин. Все потоки событий – простейшие. Определить вероятность отказа .

Задание 13

На автозаправочной станции 1 колонка. Площадка при станции допускает пребывание в очереди двух машин; если она занята, то прибывшая к станции машина проезжает мимо. Поток машин, прибывающих для заправки, имеет интенсивность 0,2 (машин в минуту). Процесс заправки продолжается в среднем 10 минут. Определить вероятность отказа.

Задание 14

На автозаправочной станции две колонки. Площадка при станции допускает пребывание в очереди 1 машины; если она занята, то прибывшая к станции машина проезжает мимо. Поток машин, прибывающий для заправки, имеет интенсивность 0,2 (машины в минуте). Процесс заправки продолжается в среднем 5 минут. Определить вероятность отказа (т.е. вероятность того, что машина, прибывшая для заправки, проедет мимо).

Задание 15

На железнодорожную сортировочную горку прибывают составы с интенсивностью 2 (состава в час). Среднее время, в течение которого горка обрабатывает состав, равно 0,4 часа. Составы, прибывшие в момент, когда горка занята, отправляются в другое место. Определить вероятность того, что прибывший состав будет разгружен на данной горке.

Задание 16

В телефонное справочное бюро поступают запросы с интенсивностью 3 (за минуту), среднее время ответа на вопрос 1 мин. Какова вероятность дозвонится и получить справку с первого раза, если работают параллельно три телефонистки?

Поиск по сайту: