 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема 7: Нелинейное программирование
Задание 1
Составить модель задачи по определению оптимального плана производства n типов машин при заданных объемах  ресурсов, норм расхода
ресурсов, норм расхода  (i=1,…, m, j=1,..., n) i-го ресурса на производство j-й машины и величинах
(i=1,…, m, j=1,..., n) i-го ресурса на производство j-й машины и величинах  (j=1, …, n) прибыли при реализации одной машины j-ого вида. Предполагается, что к концу планируемого периода не должно быть незавершенного производства.
(j=1, …, n) прибыли при реализации одной машины j-ого вида. Предполагается, что к концу планируемого периода не должно быть незавершенного производства.
Решение
Задание 2
Имеются суда m типов в количествах  , на каждом из которых имеются n грузовых емкостей с грузоподъемностью
, на каждом из которых имеются n грузовых емкостей с грузоподъемностью  . Подлежат перевозке p типов грузов в количестве
. Подлежат перевозке p типов грузов в количестве  . Составить математическую модель задачи по выбору оптимального состава судов, если затраты по эксплуатации одного судна i-ого типа равны
. Составить математическую модель задачи по выбору оптимального состава судов, если затраты по эксплуатации одного судна i-ого типа равны  .
.
Решение
Задание 4
Используя метод множителей Лагранжа, найти максимальное значение следующих функций:
1)  при ограничении
при ограничении 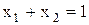
Решение
Составим функцию Лагранжа:
Продифференцируем ее по переменным
Приравнивая полученные выражения нулю, получим следующую систему уравнений:
Решим полученную систему:
Ответ:
2)  при ограничении
при ограничении  .
.
Решение
Составим функцию Лагранжа:
Продифференцируем ее по переменным
Приравнивая полученные выражения нулю, получим следующую систему уравнений:
Решим полученную систему:
Ответ:
3)  при ограничении
при ограничении  .
.
Решение
Составим функцию Лагранжа:
Продифференцируем ее по переменным
Приравнивая полученные выражения нулю, получим следующую систему уравнений:
Решим полученную систему:
Ответ:
4)  при ограничении
при ограничении  .
.
Решение.
1) Ищем стационарные точки для безусловного экстремума. Для этого продифференцируем Z по ее переменным:
Приравниваем полученные выражения к нулю и решаем систему
Находим значения функции Z в точках, удовлетворяющих ограничениям:
2) Составим функцию Лагранжа:
Продифференцируем ее по переменным
Приравнивая полученные выражения нулю, получим следующую систему уравнений:
Решим полученную систему:
Сравним результаты 1) и 2)
Ответ:
5) 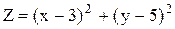 при ограничении
при ограничении  .
.
1) Ищем стационарные точки для безусловного экстремума. Для этого продифференцируем Z по ее переменным:
Приравниваем полученные выражения к нулю и решаем систему
Находим значения функции Z в точках, удовлетворяющих ограничениям:
2) Составим функцию Лагранжа:
Продифференцируем ее по переменным
Приравнивая полученные выражения нулю, получим следующую систему уравнений:
Решим полученную систему:
Сравним результаты 1) и 2)
Ответ:
Задание 5
В области решений системы неравенств 2x+5y≤30, 2x+y≤14, x≥0, y≥0 определить глобальные экстремумы функций: а)  ; б)
; б) 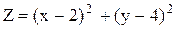 .
.
Решение
а) Построим область допустимых решений.
| 1: | A | B | 2: | A | B | |
| x | x | |||||
| y | y |
Построим линию уровня:
Линия - _______________________________________________________
__________________________________________________________________
__________________________________________________________________
Получим систему и решим ее:
Ответ:
б) Область допустимых решений такая же, что и в а).
Построим линию уровня:
Линия - _______________________________________________________
__________________________________________________________________
__________________________________________________________________
Получим систему и решим ее:
Ответ:
Задание 6
В области решений системы неравенств 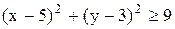 ,
,  , x+y≥8, x≥0, y≥0 определить глобальные экстремумы функций: а) z=x+3y, б) z=x+y, в)
, x+y≥8, x≥0, y≥0 определить глобальные экстремумы функций: а) z=x+3y, б) z=x+y, в)  , г) z=xy.
, г) z=xy.
Решение
а) Построим область допустимых решений.
Построим линию уровня:
Линия - _______________________________________________________
__________________________________________________________________
__________________________________________________________________
Получим систему и решим ее:
Ответ:
б) Область допустимых решений такая же, что и в а).
Построим линию уровня:
Линия - _______________________________________________________
__________________________________________________________________
Получим систему и решим ее:
Ответ:
в) Область допустимых решений такая же, что и в а).
Построим линию уровня:
Линия - _______________________________________________________
__________________________________________________________________
__________________________________________________________________
Получим систему и решим ее:
Ответ:
б) Область допустимых решений такая же, что и в а).
Построим линию уровня:
Линия - _______________________________________________________
__________________________________________________________________
__________________________________________________________________
Получим систему и решим ее:
Ответ:
Поиск по сайту: