 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
И ее следствия
Для разрешимости задачи математического программирования (как и в любой оптимизационной задачи) необходимо, чтобы множество допустимых решений было не пусто, и целевая функция на этом множестве была ограничена сверху (если задача на максимум), либо снизу (если задача на минимум).
Теорема двойственности. Каковы бы ни были исходные данные, для задач 1 и 1* имеет место один из следующих взаимоисключающих случаев.
1. В задачах 1 и 1* имеются оптимальные векторы х и у и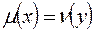 
, т.е. обе задачи разрешимы.
2. В задаче 1 существуют допустимые векторы х из некоторого множества Х, но линейная функция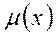 
на множестве этих векторов не ограничена сверху, т.е. 
, тогда в задаче 1* нет допустимых векторов.
3. В задаче 1* существуют допустимые векторы 
, но функция 
не ограничена снизу на множестве этих векторов, т.е.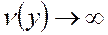 
, тогда в задаче 1 нет допустимых векторов.
4. В задачах 1 и 1* нет допустимых векторов, то есть 
Поиск по сайту: