АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Следствие из леммы 2 и признака оптимальности

Читайте также:
  1. B) наиболее часто встречающееся значение признака в данном ряду
  2. F1 Психические и поведенческие расстройства вследствие употребления психоактивных веществ
  3. II. Функции плазмолеммы
  4. III Анемии вследствие повышенного кроверазрушения (гемолитические)
  5. V. Вариационные ряды, средние величины, вариабельность признака
  6. Аллергии как следствие ослабленного кишечного барьера
  7. Альный ущерб, возникший вследствие его неправильных действий
  8. Анализ сырья по внешним признакам
  9. Анемии вследствие кровопотери (постгеморрагические)
  10. Анемии вследствие нарушения кровообразования
  11. Анемии вследствие повышенного кроворазрушения (гемолитические анемии)
  12. Б) Признака S1QIII
Задача А. Максимизировать линейную функцию на множестве n -мерных векторов х = (х1, х2,..., хn), удовлетворяющих условиям 1. 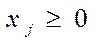, , 2. Задача А*.Минимизировать линейную функцию 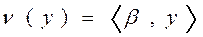на множестве m-мерных векторов y = (y1, y2,..., ym), удовлетворяющих системе линейных неравенств 1. - 2. , .

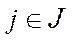Теорема. Если базисное множество К является одновременно допустимым и двойственно допустимым базисным множеством, то отвечающие ему векторы и 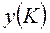оптимальные соответственно в задачах А и А*.

Доказательство. Пусть К – допустимое базисное множество и двойственно допустимое базисное множество. Это значит, что вектора и - допустимые. На основании леммы 2 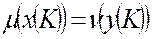, а это достаточно для того, чтобы вектор был оптимальным и вместе с ним и вектор 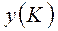(см. краткую форму достаточного признака оптимальности)▄


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)