АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Некоторые определения

Читайте также:
  1. I Определения
  2. I. Дайте определения следующих правовых категорий.
  3. I. Открытые способы определения поставщика.
  4. II. 4.4. Некоторые рекомендации по формулировке и решению задач ЦЛП
  5. II. Исследование пульса, его характеристика. Места определения пульса.
  6. III. Используемые определения и обозначения
  7. Алгоритм определения валютно-правового статуса ценных бумаг
  8. Алгоритм определения наибольшего по модулю собственного значения и соответствующего собственного вектора матрицы с положительными элементами.
  9. Алгоритм определения предпочтительной организационной структуры управления диверсифицированной фирмы
  10. Алгоритм определения точек локальных и глобальных экстремумов функции одной переменной
  11. Анализ порядка определения и формирования цены ДР.
  12. АНКЕТА ОПРЕДЕЛЕНИЯ ВОЛЕВЫХ КАЧЕСТВ У УЧАЩИХСЯ 12-16 ЛЕТ

8. Какова бы ни была прямоугольная матрица

,

 

максимальное число линейно независимых строк (т. е. со­ответствующих n-мерных векторов) совпадает с максималь­ным числом линейно независимых столбцов (т. е. соответ­ствующих m-мерных векторов). Это число называется ран­гом матрицы А. При этом квадратную матрицу

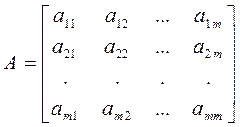
порядка m называют неособенной, если ее ранг r совпадает с m. Если отвечающая системе линейных уравнений квадратная матрица А является неособенной, то эта система имеет единственное решение при любых свободных членах .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)