АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Геометрическая интерпретация задач линейного программирования

Читайте также:
  1. I Психологические принципы, задачи и функции социальной работы
  2. I. 1.1. Пример разработки модели задачи технического контроля
  3. I. 1.2. Общая постановка задачи линейного программирования
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. 3.1. Двойственная задача линейного программирования
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  8. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  9. I. Решение логических задач средствами алгебры логики
  10. I. Розв’язати задачі
  11. I. Ситуационные задачи и тестовые задания.
  12. I. Цель и задачи дисциплины
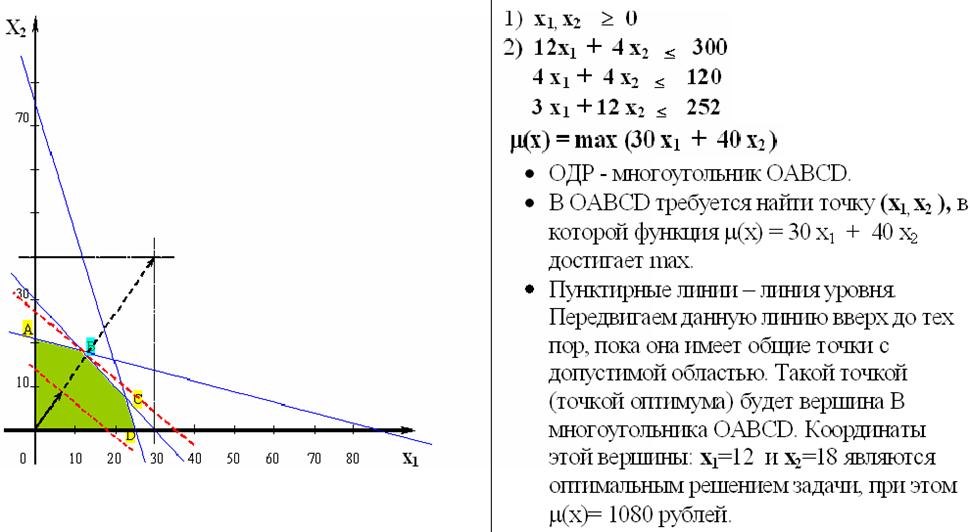
Задача планирования производства m(х) = max (30 х1 + 40 х2 ) x 1) х1, х2 ³ 0 2) 12х1 + 4 х2 £ 300 4 х1 + 4 х2 £ 120 3 х1 + 12 х2 £ 252   Основные этапы графического метода решения задач ЛП 1. Строятся прямые, уравнения которых получаются в результате замены в ограничениях 1) и 2) знаков неравенств на знаки точных равенств. 2. Находятся полуплоскости, определяемые каждым из ограничений задачи 3. Определяется область допустимых решений - ОДР (многоугольник решений) 4. Строится вектор С =(С1;С2) (C1 и C2 – коэффициенты при неизвестных в целевой функцииm(x)) 5. Строится линия уровня – как перпендикуляр к вектору С, проходящая через ОДР 6. Линия уровня передвигается в направлении вектора С (если задача поставлена на max) или в противоположном направлении (если задача поставлена на min). В результате находится либо точка оптимума (граничная точка линии уровня с ОДР), либо устанавливается неограниченность функции на множестве допустимых решений. 7. Определяются координаты точки оптимума, и вычисляется значение целевой функции в этой точке.
   

Геометрическая интерпретация задач линейного программирования


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)