АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод последовательного улучшения допустимого вектора (МПУ)

Читайте также:
  1. ERP-стандарты и Стандарты Качества как инструменты реализации принципа «Непрерывного улучшения»
  2. F. Метод, основанный на использовании свойства монотонности показательной функции .
  3. FAST (Методика быстрого анализа решения)
  4. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  5. I. 2.1. Графический метод решения задачи ЛП
  6. I. 3.2. Двойственный симплекс-метод.
  7. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  8. I. Метод рассмотрения остатков от деления.
  9. I. Методические основы
  10. I. Методические основы оценки эффективности инвестиционных проектов
  11. I. Организационно-методический раздел
  12. I. Предмет и метод теоретической экономики

II. Проверка двойственной допустимости ДБМ К. Для найденного вектора у (К) вычисляются величины и проверяются неравенства , .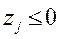

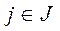1. Находим величины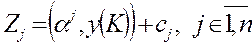

При этом возможны два случая:

а) 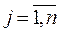. Это означает, что базисное множество К является одновременно допустимым и двойственно допустимым базисным множеством. Тогда (потеореме: если базисное множество К является одновременно допустимым и двойственно допустимым базисным множеством, то отвечающие ему векторы и 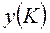оптимальные соответственно в задачах А и А*) векторы х (К) и у (К) оптимальны для соответствующих задач и 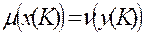. На этом процесс заканчивается с выдачей искомых оптимальных векторов.

б) условие а) нарушается, т.е. К не является двойственно допустимым и вектор не допустимый в задаче А*. Надо найти 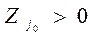и перейти к выполнению следующей процедуры.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)