АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Некоторые определения. 1. Пусть М = {a1 , a2, , аm} – множество вещественных чисел R

Читайте также:
  1. I Определения
  2. I. Дайте определения следующих правовых категорий.
  3. I. Открытые способы определения поставщика.
  4. II. 4.4. Некоторые рекомендации по формулировке и решению задач ЦЛП
  5. II. Исследование пульса, его характеристика. Места определения пульса.
  6. III. Используемые определения и обозначения
  7. Алгоритм определения валютно-правового статуса ценных бумаг
  8. Алгоритм определения наибольшего по модулю собственного значения и соответствующего собственного вектора матрицы с положительными элементами.
  9. Алгоритм определения предпочтительной организационной структуры управления диверсифицированной фирмы
  10. Алгоритм определения точек локальных и глобальных экстремумов функции одной переменной
  11. Анализ порядка определения и формирования цены ДР.
  12. АНКЕТА ОПРЕДЕЛЕНИЯ ВОЛЕВЫХ КАЧЕСТВ У УЧАЩИХСЯ 12-16 ЛЕТ

1. Пусть М = {a1, a2,..., аm} – множество вещественных чисел R

Подмножество М на­зывают ограниченным сверху, если все его элементы не пре­восходят некоторого с 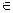R, где с называют верхней границей для М.

 

2. Для каждого ограниченного сверху непу­стого множества M 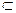R среди его верхних границ имеется минимальная, которую называют супремумом множества М и обозначают через sup M. Если же множество M 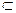R не является ограниченным сверху, то пишут sup M=+ .

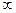Множество М 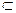R называют ограниченным снизу, если все его элементы не меньше некоторого числа с 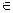R.

Соответствующие с 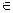R называют нижними грани­цами, а наибольшую из них — инфимумом множества М, который обозначают через inf M.

Если же множество M 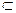R не является ограниченным снизу, то пишут

inf M =- .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)