АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод последовательного улучшения допустимого вектора (МПУ). При решении задач с помощью МПУ исходная информация и текущие данные обычно располагают в таблицах следующего вида:

Читайте также:
  1. ERP-стандарты и Стандарты Качества как инструменты реализации принципа «Непрерывного улучшения»
  2. F. Метод, основанный на использовании свойства монотонности показательной функции .
  3. FAST (Методика быстрого анализа решения)
  4. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  5. I. 2.1. Графический метод решения задачи ЛП
  6. I. 3.2. Двойственный симплекс-метод.
  7. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  8. I. Метод рассмотрения остатков от деления.
  9. I. Методические основы
  10. I. Методические основы оценки эффективности инвестиционных проектов
  11. I. Организационно-методический раздел
  12. I. Предмет и метод теоретической экономики

При решении задач с помощью МПУ исходная информация и текущие данные обычно располагают в таблицах следующего вида:

Таблица 1. Исходная информация

 

      … n  
  …
  …
  …
… … … … … … …
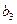
m …
  …  

Таблица 2. Текущие данные

Номер шага
k*  

Пример решения задачи ЛП с помощью МПУ

Прямая задача А Двойственная задача А*

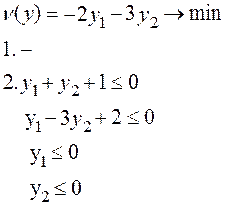
Найдем базис, базисное множество К, построим исходный допустимый вектор x (K)

α1 α2 α3 α4 β y
        -2 y1
  -3     -3 y2
сj            

Векторы α3, α4 – линейно независимы, базисное множество K ={3,4}.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)