АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Общая форма задачи ЛП

Читайте также:
  1. bending strain (майысу деформациясы)
  2. Bending strain (майысу деформациясы)
  3. CASE-технология создания информационных систем
  4. Data Mining и Business Intelligence. Многомерные представления Data Mining. Data Mining: общая классификация. Функциональные возможности Data Mining.
  5. I Понятие об информационных системах
  6. I Психологические принципы, задачи и функции социальной работы
  7. I. 1.1. Пример разработки модели задачи технического контроля
  8. I. 1.2. Общая постановка задачи линейного программирования
  9. I. 2.1. Графический метод решения задачи ЛП
  10. I. ВВЕДЕНИЕ В ИНФОРМАТИКУ
  11. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  12. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ

Пусть заданы: множества I ={1,2…m} и J= {1,2…n}, причем I= I1U I2, I1 Ç I2 = Æ, J= J1UJ2, J1Ç J2 = Æ, вещественные числа аij, iÎI, jÎJ; bi, iÎI, сj, jÎJ.

 

ЗАДАЧА 1 (прямая со смешанными ограничениями)

Максимизировать линейную функцию

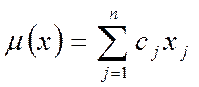(1)

на множестве векторов х= (х1,х2, …хn,), (2)

удовлетворяющих условиям:

 

1. хj ³0 для jÎJ2 (3)

2. 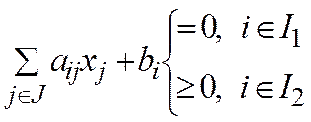(4)

 

Двойственная задача ЛП

ЗАДАЧА 1* (двойственная со смешанными ограничениями).

Минимизировать линейную функцию

(5)

на множестве векторов y= (y1,y2,…..ym), (6)

удовлетворяющих условиям:

1. yi ≥ 0 для iÎI2 (7)

2. (8)

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.007 сек.)