Пример 1. Рассмотрим в качестве минимизируемой функции ( ) функцию Розенброка (

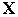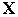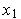Рассмотрим в качестве минимизируемой функции () функцию Розенброка ( =2). Положим, что имеется только одно ограничение типа равенств, которое задается с помощью функции ()= + +0.2=0. Легко видеть, что градиенты функций (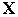), (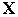) равны, соответственно

Задачу иллюстрирует рис. 2, линии уровня функции Розенброка на котором получены с помощью следующей MATLAB-программы:

x=-2:0.06:0;

y=x;

[X,Y]=meshgrid(x);

Z=100.*(Y-X.^2).^2+(1-X).^2;

V=[2,8,32,125,250,500,1000,2000];

contour(X,Y,Z,V);

[C,h]=contour(X,Y,Z,V);

clabel(C,h);

В точках , векторы градиента функций , (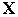) не коллениарны. Поэтому для этих точек не существует не равный нулю множитель Лагранжа , при котором функция Лагранжа равна нулю: . И поэтому точки , не могут быть точками локального минимума для рассматриваемой задачи. Наоборот, в точке векторы градиента функций , коллениарны и поэтому существует не равный нулю множитель , при котором справедливо равенство 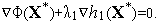Отметим, что, например в точке , градиент функции Розенброка равен

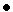
Рис. 2. K прим. 1.

Теорема 1 означает, что в ее условиях вместо задачи условной оптимизации (1), (2) можно решать задачу безусловной оптимизации

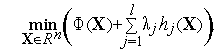
Необходимым условием существования локального минимума этой задачи в некоторой точке 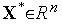является условие (см. Теорему 2.1).

Широко известна другая форма теоремы 1, которую мы сформулируем в виде следствия этой теоремы.

Следствие. В условиях теоремы 1 существуют такие множители Лагранжа , не все из которых равные нулю одновременно, что имеют место следующие равенства:

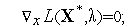
(12)

(13)

Здесь равенство (12) повторяет равенство (4), а справедливость равенства (13) следует из того факта, что по условиям теоремы точка 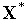удовлетворяет всем ограничениям, т.е. .

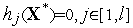Заметим, что из (13) следует справедливость еще одного полезного равенства

Поиск по сайту: