Теорема (принцип максимума Понтрягина)

Пусть функции f 0, f 1,..., fn и, Ф, g 1,..., gm имеют частные производные

по переменным x 1,..., xn и непрерывны вместе с этими производными по

совокупности аргументов . Предположим, что (u, x) –

решение задачи (8.2). Тогда существует решение 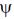сопряженной системы

(8.4), соответствующей управлению u и траектории x, и константа

такие, что 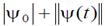при 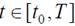, и выполняются следующие условия:

a) (условие максимума) 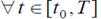функция Гамильтона

достигает максимума по при v = u (t), т.е.

б) (условие трансверсальности на левом конце траектории) существуют

числа 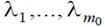, такие, что:

в) (условие трансверсальности на правом конце траектории) существуют числа 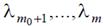, такие, что:

Центральным в теореме является условие максимума – (8.5).

Если отказаться от предположения о том, что конечный момент времени T фиксирован, то теорема останется справедливой за исключением условия трансверсальности на правом конце траектории. Условие (8.7)необходимо заменить условием:

и добавить еще одно условие трансверсальности на правом конце

траектории:

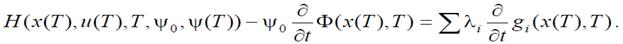
9. Оптимальное по быстродействию управление линейными объектами.

Оптимизационные задачи с нефиксированных времени tk в функционале качества наз. Задачами быстродействия.

Математическая постановка задачи:

Дано:математическая модель объекта в виде x^/ = Ax+Bu,где A-матрица [n*n], u-скалярное число, Bматрица [n*1].

x_i^/=a_i1*x₁+ a_i2*x₂+….+ a_in*x_n ,
……………..

x_n^/=a_n1*x₁+ a_n2*x₂+….+ a_{n n}*x_n +k_u

граничные условия

x_i(0)=x_i0

x_i(T)=x_iT -_{- эти 2 условия взять в} {

I= стремящийся к extr

│ U(t)│≤Umax

Требуется определить оптимал. Программное управление воздействия U(t)переводящая объект управления из начального положения x_i0 в конечное x_iT за миним. время.

Решение

Поскольку необходимо и достаточно условию оптимальности при решении задач быстродействия является принцип таксим., то для решения необходимо составить функцию гамельтона.

H(x, Ψ,u)= Ψ₀₁+ Ψ _i (t)(a_i1*x₁+ a_i2*x₂+….+ a_{i n}*x_n )+Ψ_n(t)(a_n1*x₁+ a_n2*x₂+….+ a_{n n}*x_n +k_u)стремящийся к max

Искомый закон управления U(t)определяется из условия достижения max функции Гамильтона пред полагаемых на управляющие воздействия ограничении. В рассматриваемых случаях функции Гамильтона является линейной относит. управляющего воздействия, тогда ӘH / Әu= Ψ_n(t)*k неравно 0

Поэтому функция Гамильтона достигает своего максимума значения на границах интервала ограничений управляющий воздействия.

Из выражения ӘH / Әu следует, что макс Гамильтона зависит только от знака производной функции Гамильтона.

U=U_max*sign ӘH / Әu=sign (k Ψ_n)

Полученный закон уравнения справедлив в каждый момент времени принадлежащий интервалу управления решения.

Функция Ψ^*(t)определяется из системы сопряженных уравнений в соответствии со 2-ом условием теоремы принципа максимума. Моменты смена знака управляющего воздействия U(t) совпадают с моментами времени T_i перехода Ψ _i через 0.Эти моменты T_i заранее не известны, а так же их количество заранее не определено.Теорема об n-интервале позволяет их найти.

10. Способы нахождения экстремума функции двух переменных.

Говорят, что функция z=f(x,y) имеет максимум в точке M₀(x₀,y₀), т.е. при x=x₀, y=y₀, если f(x₀,y₀)> f(x,y) для всех точек (x,y), достаточно близких к точке (x₀,y₀) и отличных от неё.

Говорят, что функция z=f(x,y) имеет минимум в точке M₀(x₀,y₀), т.е. при x=x₀, y=y₀, если f(x₀,y₀)< f(x,y) для всех точек (x,y), достаточно близких к точке (x₀,y₀) и отличных от неё.

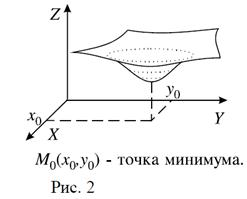
Максимум и минимум функции называются экстремумами функции.

Теорема (необходимое условие экстремума функции двух переменных). Если функция z=f(x,y) достигает экстремума при x=x₀, y=y₀ , то каждая частная производная первого порядка от z или обращается в нуль при этих значениях аргументов, или не существует.

Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку M₀(x₀,y₀) функция z=f(x,y) имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка M₀(x₀,y₀) является критической точкой функции f(x,y), т.е.

,

тогда при x=x₀, y=y₀:

1) f(x,y) имеет максимум, если дискриминант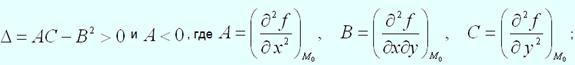

2) f(x,y) имеет минимум, если дискриминант

3) f(x,y) не имеет ни минимума, ни максимума, если дискриминант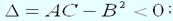

4) если , то экстремум может быть, а может и не быть (требуется дополнительное исследование).

Поиск по сайту: