Дифракционная решётка как спектральный прибор. Выше мы рассматривали дифракцию в случае монохроматического излучения

Выше мы рассматривали дифракцию в случае монохроматического излучения. Когда на решетку падает свет сложного спектрального состава, то на экране, на месте главных максимумов (кроме центрального) наблюдаются спектры, соответственно 1-го, 2-го и т.д. порядков. При этом фиолетовые лучи в каждом спектре отклоняются меньше, чем красные (). Это определяется зависимостью угла дифракции, для которого наблюдается главный максимум, от длины волны.

Пусть на дифракционную решётку падает плоская световая волна, представляющая собой суперпозицию трех световых пучков с длинами волн 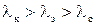. Распределение интенсивностей и дифракционная картина, получающиеся в результате дифракции имеют вид, представленный на рис.19а,б.

На экране (рис.19б) спектры различных порядков разделены темными промежутками, но иногда могут накладываться друг на друга. Таким образом, дифракционная решетка представляет собой спектральный прибор.

Основными характеристиками любого спектрального прибора являются дисперсия и разрешающая способность.

Дисперсия определяет линейное или угловое расстояние, на которое будут разведены диспергирующим элементом два пучка света, отличающиеся по длине волны на единицу (например, на 1 нм).

Угловой дисперсией называется величина

, (14)

где – угловое расстояние между двумя спектральными линиями, отличающимися по длине волны на .

Положение главных максимумов для дифракционной решетки определяется из условия . Продифференцировав последнее равенство по длине волны получаем

.

При небольших углах дифракции () и

. (15)

Из (15) следует, что чем выше порядок спектра, тем больше дисперсия. Дисперсия также больше при наблюдении спектра с помощью дифракционной решетки с меньшим периодом.

Разрешающая способность определяет минимальную разность длин волн , при которой линии спектра воспринимаются раздельно

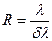. (16)

Рис.20

Согласно критерию Релея, спектральные линии считаются полностью разрешёнными, если середина одного максимума совпадает с краем другого максимума (рис.20). В этом случае минимум между линиями составляет 80% от максимумов.

Пусть на дифракционную решётку падают две волны: и . При порядке дифракции максимумы этих двух волн будут разрешены по критерию Релея, если максимум одной волны совпадает с краем максимума другой.

Запишем условие максимума для излучения с длиной волны

,

для излучения с длиной волны 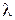– условие дополнительного минимума

.

Так как , то 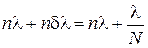. Из последнего выражения получаем

, (17)

где – порядок спектра, – число щелей решетки.

Из (17) следует, что лучше разрешаются линии в спектрах более высоких порядков, и большей разрешающей способностью обладают решетки с большим числом щелей.

Из условия максимума для дифракционной решётки , следует, что при угле дифракции и максимальный порядок спектра решетки 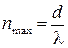. Отсюда можно получить, что максимальная разрешающая способность решетки

, (18)

где 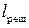– длина дифракционной решетки.

Поиск по сайту: