Дифракция Фраунгофера на дифракционной решётке

Одномерная дифракционная решётка представляет из себя систему параллельных щелей равной ширины, лежащих в одной плоскости и разделённых равными по величине непрозрачными промежутками.

Величина называется периодом дифракционной решётки.

Рассмотрим падение на дифракционную решётку плоской монохроматической световой волны, волновой фронт которой совпадает с плоскостью решётки.

По принципу Гюйгенса-Френеля каждая щель – часть волновой поверхности – излучает вторичные волны в сторону экрана наблюдения. Фаза волн в плоскости решетки для всех щелей одинакова. Интенсивность в произвольной т. P на экране будет результатом наложения волн, идущих от всех щелей.

Если первая щель в точке наблюдения создаёт колебание , то вторая щель в точке наблюдения создаёт колебание . Аналогично , …, , где – разность фаз между волнами, идущими от соседних щелей.

Результирующее колебание в точке наблюдения определяется суперпозицией колебаний, создаваемых отдельной щелью:

,

где – комплексная амплитуда колебаний в точке наблюдения, – количество щелей в дифракционной решетке.

Интенсивность света на экране наблюдения определяется квадратом амплитуды результирующего колебания:

(10)

Интенсивность дифракционного поля можно получить из исследования последней формулы, т.е. зависимости интенсивности от угла дифракции.

а) Из формулы видно, что интенсивность обращается в ноль при условии

, (11)

Полученное условие называется условием главных минимумов для дифракционной решетки и соответствует условию минимума при дифракции от одной щели. Таким образом, минимум для щели является также минимумом для решетки.

б) Интенсивность также обращается в ноль, если

, , (12)

– количество щелей дифракционной решётки.

Выражение является условием минимума для дифракционной решетки и определяет положение вторичных минимумов интенсивности.

в) В случае, когда

, , (13)

функция (10) будет принимать максимальное значение.

Третье условие определяет положение главных максимумов при дифракции на дифракционной решётке и называется условием для главных максимумов.

Из вышеприведенных условий следует, что между двумя соседними главными максимумами располагается дополнительных минимумов и соответственно дополнительных максимумов. Интенсивность дополнительных максимумов незначительна, они лишь создают некоторый фон на экране.

Таким образом, распределение интенсивности и дифракционная картина, получающиеся от решетки имеют вид, представленный на рис.17а,б. Пунктирная кривая, проходящая через вершины главных максимумов, изображает интенсивность от одной щели, умноженную на 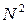. При указанных на графике параметрах решетки главные максимумы 2-го, 4-го и т.д. порядков пропадают, так как они накладываются на минимумы от одной щели. При наблюдении в монохроматическом свете на экране виден ряд ярких полос, разделенных темными промежутками.

При изменении параметров дифракционной решетки, получающиеся распределение интенсивности и дифракционная картина будут меняться (рис18а,б).

Поиск по сайту: