Дифракция Френеля на полуплоскости

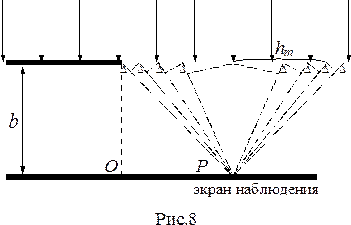На пути плоской световой волны помещён непрозрачный экран с прямолинейным краем таким образом, чтобы плоскость экрана совпадала с волновой поверхностью.

Согласно принципу Гюйгенса-Френеля, на открытой части волновой поверхности образуются точечные источники вторичных волн. Открытую часть волновой поверхности разбиваем на зоны, имеющие вид прямолинейных полосок, параллельных краю экрана (рис.8).

Ширину полос выбираем таким образом, чтобы разность хода лучей от краёв соседних полос была одинаковой и равнялась . В этом случае колебания, создаваемые в т. P соседними зонами, будут сдвинуты по фазе на постоянную величину .

Суммарная ширина первых m зон определяется из прямоугольного треугольника (см. рис.8) и равна:

Отсюда, ширина первой зоны согласно последней формуле будет равна: ,а ширина m первых зон . Из последнего выражения следует, что ширина m -ой зоны

.

При вычислении можно получить: . Это говорит о том, что при переходе от одной зоны к другой их площади и, соответственно, амплитуды излучаемых полей убывают сначала быстро, а потом медленно.

Амплитуды колебаний, создаваемые в т. P вторичными источниками различных зон изобразим на векторной диаграмме (рис.9а).

Правая часть векторной диаграммы соответствует полю излучения зон, расположенных на волновой поверхности справа от т. P, а левая половина – слева от т. P.

Если ширину зон устремлять к нулю, то ломаные линии на векторной диаграмме превращаются в плавную кривую, которую называют спиралью Корню (рис.9б). Спираль Корню даёт возможность найти амплитуду световой волны в любой точке экрана.

Для точки наблюдения все зоны, расположенные справа, являются открытыми, а зоны слева закрываются непрозрачным экраном. Колебания открытых зон справа дают правый завиток спирали Корню, и результирующее колебание представляет собой суперпозицию колебаний всех открытых зон, которое на векторной диаграмме изображается в виде вектора, проведённого из точки в фокус спирали .

При перемещении точки наблюдения P влево непрозрачным экраном будут перекрываться первые зоны излучения, расположенные справа на векторной диаграмме. Таким образом, конец вектора, изображающего амплитуду результирующего колебания, будет оставаться в фокусе спирали , а начало вектора будет скользить по правому завитку спирали с уменьшением амплитуды.

При перемещении точки наблюдения вправо начинают открываться зоны слева от точки наблюдения, и начало результирующего вектора начинает скользить по левому завитку спирали. При этом длина вектора будет колебаться при переходе от одной зоны спирали к другой.

Вектор, проведённый из одного фокуса в другой, будет соответствовать случаю, когда открыты все зоны справа и слева от точки наблюдения.

Исходя из вышесказанного, зависимость интенсивности света и дифракционная картина на экране наблюдения от координаты x (положения точки наблюдения) будет иметь вид, показанный на рисунке (рис.10).

Поиск по сайту: