Дифракция Френеля на диске

Рассмотрим падение сферической волны, распространяющейся в изотропной однородной среде от точечного источника , на непрозрачный диск радиуса . Точка наблюдения расположена против центра отверстия. Обозначим через 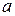– расстояние от источника до волновой поверхности, b – расстояние от волновой поверхности до точки наблюдения (рис.7).

Открытую для точки наблюдения часть волновой поверхности разобьем на зоны, называемые зонами Френеля (см. выше). Если диск закрывает m первых зон Френеля, то амплитуда результирующего колебания в точке P запишется следующим образом:

При небольших значениях m амплитуды колебаний, возбуждаемых в соседних точках, приблизительно одинаковы и амплитуда колебания в т. .

Таким образом, интенсивность света в т. такая же, как и в отсутствие преграды.

При смещении точки наблюдения от положения симметрии, аналогично вышеизложенному случаю – дифракции на круглом отверстии, мы будем проходить последовательность минимумов и максимумов интенсивности, и дифракционная картина будет представлять чередование светлых и тёмных колец, причём в центре всегда будет светлое пятно. Если диск закрывает лишь небольшую часть волновой поверхности, дифракционная картина будет такой же, как и в отсутствие преграды. Если диск закрывает большую часть волновой поверхности, чередование светлых и темных колец наблюдается в узкой области вблизи границы геометрической тени. Поскольку в этом случае амплитуда , освещённость в области геометрической тени практически отсутствует.

Поиск по сайту: