 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Неоклассические теории экономического роста. Неоклассические модели экономического роста разрабатывались на основе использования производственных функций
Неоклассические модели экономического роста разрабатывались на основе использования производственных функций, т.е. функций, устанавливающих зависимость между выпуском продукции и факторами производства. Обычно исследователи исходят из предпосылки эффективного использования факторов. Например, из всего множества комбинаций труда и капитала, удовлетворяющих бюджетным возможностям фирмы, анализ останавливается на множестве комбинаций факторов, соответствующих полному использованию бюджета (граничная линия на графике бюджетных возможностей фирмы).
Производственная функция
Производственные функции могут отражать зависимость выпуска от любого количества факторов и иметь различный вид. Например, это может быть математическая модель межотраслевого баланса (производственная функция Леонтьева, использованная Р. Харродом) или модели линейного программирования (для максимизации выпуска на выпуклом множестве производственных возможностей для большого числа факторов).
Рассмотрим производственную функцию в общем виде Y = f (K,L) и определим свойства производственных функций. Производственная функция строится таким образом, чтобы удовлетворить следующим гипотезам (временно абстрагируемся от технического прогресса).
1) Непрерывность. Функции являются непрерывными и превращаются в нуль, когда один из производственных факторов превращается в нуль:
f (0,L) = f (K,0) = 0.
2) Аддитивность. Это означает, что объединение усилий двух групп (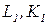 ) и (
) и (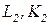 ) даст результаты по меньшей мере такие же хорошие, как и результаты, достигнутые при раздельном производстве этих групп; кооперация групп не может дать худшие результаты:
) даст результаты по меньшей мере такие же хорошие, как и результаты, достигнутые при раздельном производстве этих групп; кооперация групп не может дать худшие результаты:
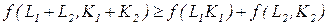 .
.
3) Делимость. Гипотеза делимости означает, что любой производственный процесс может осуществляться в сокращенных масштабах. Из закона падающей предельной производительности факторов производства при росте его объемов следует:
 .
.
Используя указанные три гипотезы, можно вывести некоторые важные свойства производственных функций.
Свойство 1. Постоянная отдача.
Удвоение факторов производства, например, приводит к удвоению выпуска продукции:
 . (8.8)
. (8.8)
Если опустить гипотезы 2 и 3, то кроме постоянной отдачи можно было бы получить возрастающую и убывающую отдачу:
 ,
,
возрастающая отдача при h > 1;
постоянная отдача при h = 1;
убывающая отдача при h < 1.
При постоянной отдаче выражение (1) можно заменить следующим уравнением:
 , (8.9)
, (8.9)
где 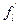 и
и  есть предельная отдача труда и капитала.
есть предельная отдача труда и капитала.
Используя свойство постоянной отдачи, можно свести функцию f(L,K) к функции с одной переменной, записав ее в виде Y/L = f(1,K/L), или в виде
 , (8.10)
, (8.10)
где x=K/L 
Свойство 2. Падение предельной производительности.
Это свойство известно из экономической теории, когда один фактор из двух увеличивается, то его предельная производительность снижается (свойство постоянной отдачи соблюдается при увеличении двух факторов в одинаковой пропорции).
Производственная функция Кобба-Дугласа – это производственная функция, которая учитывает совокупность двух основных факторов производства – капитала и труда и обладает установленными выше свойствами. В соответствии с общим свойством всех производственных функций данная функция предполагает полное использование капитала и полную занятость.
Функция Кобба-Дугласа была введена двумя американскими экономистами – Ч. Коббом и П. Дугласом – для изучения замены факторов «труд-капитал»: 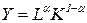 , где 0<
, где 0<  <1.
<1.
Функция может быть переписана в виде  или
или
 , (8.11)
, (8.11)
где y=Y/L;
k=K/L.
Графическое изображение функции Кобба-Дугласа в форме (8.11) имеет следующий вид (рис. 8.3).
 |
Рассмотрим произвольную точку А функции, касательную к этой точке и прямую 0b, проведенную через начало координат параллельно касательной. Тогда:
выпуск продукции = L 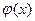 = L(ab);
= L(ab);
доля оплаты труда в выпуске = L 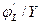 =
=  ;
;
доля капитала в выпуске – K 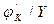 =1-
=1-  .
.
Поскольку прямая 0b параллельна касательной, то можно показать, что отрезок аА разбивается прямой 0b пропорционально доле труда (bA) и капитала (ab) в выпуске.
Рассмотрим эластичность замены в функции Кобба-Дугласа. Поскольку изокванты (кривые, точки которых есть сочетание L и К, для которых производственная функция принимает одни и те же значения)представляют собой непрерывные кривые, замена возможна при условии 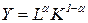 =constant.
=constant.
Кроме того, при замещении факторов должны сохраняться пропорции их долей в выпуске. Отсюда следует, что эластичность замены в функции Кобба-Дугласа равна 1[14].
Отношение  /(1-
/(1-  ) в функции Кобба-Дугласа остается постоянным. Если, например,
) в функции Кобба-Дугласа остается постоянным. Если, например,  =0,3, то вклад труда в Y составляет 30%.
=0,3, то вклад труда в Y составляет 30%.
Существует еще один фактор, помимо труда и капитала, который вызывает рост производства – технический прогресс. Этот термин отражает не только технологическое обновление производства на основе использования более производительной техники или новых материалов, но и все другие причины, которые влияют на отдачу труда и капитала (более совершенная организация труда, улучшение качества рабочей силы, улучшение отраслевой структуры производства, повышение эффективности государственного управления и пр.)
В производственной функции технический прогресс задается экзогенным параметром
 или, в общем виде, Y =A(t)F(L,K),
или, в общем виде, Y =A(t)F(L,K),
где параметр  , или A(t), задает постоянный во времени темп роста выпуска, вызванный техническим прогрессом.
, или A(t), задает постоянный во времени темп роста выпуска, вызванный техническим прогрессом.
Поиск по сайту: