 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Долгосрочный спрос на инвестиции Критерии чистой дисконтированной стоимости
Обсуждая межвременное бюджетное ограничение в вопросе 3, мы видели, что точка его пересечения с горизонтальной осью характеризует приведенную ценность двухпериодной комбинации доходов, на которую рассчитывает индивид, т. е. измеряет максимально возможную величину сегодняшнего потребления, соответствующую данному потоку его текущего и будущего дохода.
Понятие приведенной ценности оказывается незаменимым средством для осмысления проблем, в которых присутствует задача соизмерения или сравнения разнесенных во времени доходов и расходов. Например, учеба в университете стоит немалых расходов в настоящем, но влечет за собою получение дополнительных доходов в течение многих лет в будущем. Как решить, оправдывают ли будущие доходы сегодняшние расходы?
В этом вопросе мы рассмотрим концепцию приведенной ценности, а в следующем используем ее для ответа на поставленный выше вопрос. Предположим, что вы отнесли свои 100 тыс. руб. в банк и поместили их на счет, приносящий 14% в год. В конце года вы будете иметь (1+ 0.14) 100 тыс. руб. = 114 тыс. руб., т.е. 100 тыс. руб. основной суммы и 14 тыс. руб. процентов. Пусть вы оставили деньги на счете на следующий год. В конце второго года вы будете иметь (1 + 0.14)114 тыс. руб. = 129.96 тыс. руб. Этот результат можно получить следующим образом: (1 + 0.14)(1 +0.14)100 тыс. руб. = (1 + 0.14)2*100 тыс. руб. Аналогично, если деньги оставлены на банковском счете в течение трех лет, они вырастут за три года до (1 + 0.14)3 *100 тыс. руб.
Итак, если мы вкладываем М руб. на Т лет при неизменной ставке годового процента i, то в конце Т-го года мы будем иметь М(1 + i)Т руб. Эта формула показывает будущую ценность денег, инвестируемых сегодня.
Теперь предположим, что кто-то предлагает вам заключить договор, согласно которому вам обязаны заплатить 100 тыс. руб. через год после заключения договора. Причем обязательство берет на себя абсолютно надежное лицо и вы можете не опасаться его неплатежеспособности. Пусть инфляция отсутствует, чтобы наши расчеты были проще. Какую максимальную сумму вы готовы заплатить сегодня, чтобы приобрести право, предоставляемое договором?
Если кто-то скажет, что такое обещание заплатить 100 тыс. руб. имеет ценность 100 тыс. руб., то он ошибется, поскольку упустит из вида то, что обещанные 100 тыс. руб. будут уплачены через год. Платить же за договор нужно сегодня, поэтому вы потеряете процент, который могли бы заработать за год, поместив сегодня свои деньги на счет в банке. Разумно ли платить сегодня 100 тыс. руб. за приобретение через год 100 тыс. руб., если вы можете, поместив ту же сумму на счет в банке, иметь через год 114 тыс. руб.? Следовательно, 100 тыс. руб., которые будут получены через год, сегодня ценятся меньше, чем 100 тыс. р., имеющихся сегодня.
Сегодняшняя ценность некоторой будущей суммы денег — это максимум того, что вы готовы заплатить сегодня за право получить в будущем данную сумму денег. А именно, это столько, что, будучи умноженным на 1+0.14, оно становится равным 100 тыс. руб. В этом случае рассматриваемый договор будет для вас привлекателен не меньше, чем помещение денег в банк.
Обозначим PV приведенную ценность договора. Сформулированное только что условие будет выглядеть так:
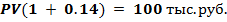
Следовательно, приведенная к настоящему моменту времени ценность оговоренной суммы равна
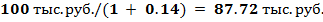
Итак, чтобы найти будущую (через год) ценность сегодняшней суммы денег, нужно умножить ее (сумму) на 1 + i, а чтобы найти приведенную ценность будущей (наличной через год) суммы денег, нужно разделить ее на 1 + i.
В общем случае, когда годовая ставка процента равна i, сегодняшняя ценность грядущей через Т лет суммы М равна М/(1 + i)T. Следовательно, даже при отсутствии инфляции будущий рубль представляет собой сегодня меньшую ценность, чем рубль сегодняшний. Поэтому любую будущую сумму денег (как доходов, так и расходов) необходимо дисконтировать (уменьшать) с коэффициентом, зависящим от ставки процента и срока, по истечении которого эта сумма окажется в наличии. По этой причине i часто называют нормой дисконта.
Представим себе абсолютно надежное обещание потока доходов, состоящего из M0 (рублей) сегодня, М1 через год, M2 через два года и т. д. на Т лет. Как высоко ценится такое обещание (обязательство)? Теперь нам понятно, что наивный ответ 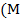 о
о 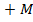 1
1 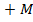 2
2 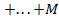 T
T 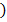 неверен. Приведенная к настоящему моменту ценность указанного потока доходов равна
неверен. Приведенная к настоящему моменту ценность указанного потока доходов равна
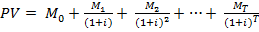 (9.11)
(9.11)
Приведем некоторые примеры использования концепции приведенных затрат для анализа конкретных ситуаций.
1) Предположим, что вы вознамерились купить квартиру, но не имеете сегодня необходимых для этого 175 млн руб., поэтому подумываете о том, чтобы взять в банке эту сумму в кредит под залог квартиры (кредит по закладной). Банк предлагает вам на выбор два варианта закладной. По варианту А вы должны ежегодно выплачивать 14 млн 600 тыс. руб. в течение 30 лет. По варианту Б вы должны ежегодно выплачивать 19 млн 720 тыс. руб. в течение 15 лет. Если просто просуммировать деньги, которые предстоит выплатить за весь срок кредита, то по варианту А получится 438 млн руб., а по варианту Б — 295 млн 800 тыс. руб.
Многим покажется, что выплаты по закладной — это грабеж средь бела дня. Почему нужно платить так много за 175- миллионный кредит? Даже «более дешевый» вариант Б стоит без малого 300 млн руб.! Не лучше ли быстрее покинуть банк с чувством, что вы сэкономите кучу денег? Верны ли такие рассуждения? Концепция приведенной ценности утверждает — нет.
175 млн руб. вы получите сегодня, а выплачивать деньги в погашение долга вам придется в будущем, в том числе в будущем весьма отдаленном. Пусть альтернативная ценность денежных фондов, доступных вам, равна 7.5% в год. При такой норме дисконта сегодняшняя ценность всех выплат по 30-летней закладной равна 172 млн 432 тыс. руб., а сегодняшняя ценность всех выплат по 16-летней закладной составит 174 млн 71 тыс. руб. Получается, что вам есть смысл взять кредит. При этом заметим, что закладная с 15- летним сроком вовсе не лучше, так как стоит дороже. Правда, если ваша норма дисконта будет ниже, закладная с меньшим сроком может оказаться предпочтительнее. Таким образом, вывод о приемлемости условий кредита, сделанный с учетом дисконтирования будущих выплат, отличается от первоначального наивного суждения. Трудно переоценить важность исчисления сегодняшней ценности будущих доходов и расходов для принятия правильных решений.
2) Рассмотрим еще один пример. Чтобы консолидировать долги, вызванные войной с Наполеоном, британское правительство выпустило облигации, называемые консолями, по которым в каждом будущем периоде выплачивалась фиксированная сумма. Консоль является примером пожизненной ренты (ренты на неограниченный срок). Какова приведенная ценность пожизненной ренты?
Оказывается, ее очень просто определить, если ставка процента остается неизменной. Пусть фиксированная сумма денег, выплачиваемая ежегодно, равна М, а годовая ставка процента — i. Чтобы определить приведенную ценность пожизненной ренты, нужно определить сумму денег, которая, будучи помещенной в банк под процент i, приносила бы ежегодно процентный доход М. Эта сумма, PV, определяется из решения уравнения 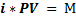 ; следовательно,
; следовательно,
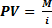 (9.12)
(9.12)
Мы можем получить тот же результат иначе, использовав обобщение формулы (9.11) для бесконечного срока Т, т. е. определить сумму бесконечной геометрической прогрессии:
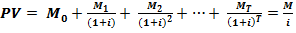 (9.13)
(9.13)
Если, например, годовая ставка процента равна 5%, приведенная к начальному моменту ценность пожизненной ренты в 250 ф. ст. равна 5000 ф. ст.
Хотя в современной практике консоли уже не используются, уравнение (9.12) чрезвычайно полезно по двум причинам.
Во-первых, некоторые активы, такие как земля, приносят доходы бесконечно долго, и формула (9.12) помогает оценить их.
Во-вторых, уравнение (9.12) может быстро дать приблизительное значение приведенной ценности потока доходов, поступающих в течение конечного числа лет, если это число велико.
Предположим, вы оцениваете поток доходов, ожидающийся в следующие 20 лет, причем годовая ставка процента равна 12%. Применять формулу (9.10) несложно, но утомительно. Проще и быстрее воспользоваться формулой (9.11). Результат будет хорошим приближением к точному ответу. Разумеется, погрешность зависит от величины ставки процента и числа лет. Чем меньше ставка процента и чем больше число лет, тем точнее результат.
4) Итак, концепция приведенной ценности позволяет нам сравнивать доходы и расходы различных лет, если нам известна цена кредита (годовая ставка процента) в каждом году. Предположим, что вы оцениваете некоторый проект (например, капиталовложений), который изменяет ваши доходы и расходы в ближайшие Т лет. Чтобы определить прибыльность этого проекта, следует вычислить приведенную к начальному моменту ценность всех доходов (дисконтировав будущие доходы) и приведенную ценность всех расходов (дисконтировав будущие расходы), после чего вычесть из первой суммы вторую. Если вы получили положительную величину, ваш проект прибыльный.
Полезную информацию о проекте может дать ответ на следующий вопрос: при какой годовой ставке процента сумма дисконтированных расходов в точности равна сумме дисконтированных доходов? Такая ставка процента, делающая проект безубыточным, называется внутренней нормой дохода (IRR; internal rate of return — англ.). Обозначим доходы, приносимые проектом в году t, Rt, расходы, связанные с осуществлением проекта, 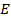 t. Тогда внутреннюю норму дохода IRR находят из решения уравнения
t. Тогда внутреннюю норму дохода IRR находят из решения уравнения
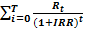 -
- 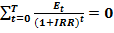 (9.14)
(9.14)
Если проект характеризуется, например, внутренней нормой дохода 16%, а у вас есть основания ожидать, что годовая ставка процента на кредитном рынке будет сохраняться на уровне 12%, то можете сделать вывод о прибыльности проекта [2, с. 338 – 343].
Поиск по сайту: