 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Имитационная модель оценки риска
Суть этого метода заключается в следующем:
1. На основе экспертной оценки по каждому проекту строят три возможных варианта развития:
а) наихудший;
б) наиболее реальный;
в) оптимистический.
2. Для каждого варианта рассчитывается соответствующий показатель NPV, т.е получают три величины: NPVН (для наихудшеговарианта); NPVР (для наиболее реального); NPVО (для оптимистического).
3. Для каждого проекта рассчитывается размах вариации (RNPV) – наибольшее изменение NPV. RNPV=NPVO-NPVH и среднее квадратичное отклонение по формуле:
 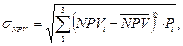 
| (5.3.1) |
 где NPVi – приведенная чистая стоимость каждого из рассматриваемых вариантов;
где NPVi – приведенная чистая стоимость каждого из рассматриваемых вариантов;
- среднее значение, взвешенное по присвоенным вероятностям (Pi);

Из двух проектов считается более рискованным тот, у которого больше вариационный размах (RNPV) или среднее квадратическое отклонение (sNPV).
Пример 1. Рассматриваются два альтернативных инвестиционных проекта А и Б, срок реализации которых 3 года. Оба проекта характеризуются равными размерами инвестиций и ценой капитала, равной 8%. Исходные данные и результаты приведены в табл. 8.3.1.
Таблица 8.3.1
(млн. руб.)
| Показатель | Проект А | Проект Б |
| Инвестиции Оценка среднегодового поступления средств: наихудшая наиболее реальная оптимистическая Оценка NPV: наихудшая наиболее реальная оптимистическая Размах вариации | 20,0 7,4 8,3 9,5 -0,93 1,39 4,48 5,41 | 20,0 7,0 10,4 11,8 -1,96 6,8 10,4 22,77 |
Несмотря на то, что проект Б характеризуется более высокими значениями NPV, тем не менее его можно считать значительно рискованней проекта А, так как он имеет более высокое значение вариационного размаха.
Проверим этот вывод, для чего рассчитаем средние квадратические отклонения обоих проектов. Последовательность действий следующая.
1. Экспертным путем определим вероятность получения значений NPV для каждого проекта (см. табл. 8.3.2).
Таблица 8.3.2
| Проект А | Проект Б | ||
| NPVj, млн.руб. | Экспертная оценка вероятности | NPVj, млн.руб. | Экспертная оценка вероятности |
| -0,93 1,39 4,48 | 0,1 0,6 0,3 | -1,96 6,8 10,4 | 0,05 0,70 0,25 |
2. Рассчитаем среднее значение для каждого проекта.
А=-0,93×0,1+1,39×0,6+4,48×0,3=2,085;
Б=-1,96×0,05+6,8×0,7+10,4×0,25=7,262.
3. Определим среднее квадратическое отклонение sNPV для каждого проекта.
sNPV=((-0,93-2,085)2× 0,1+(1,39-2,085)2× 0,6+(4,48-2,085)2× 0,3)1/2=
=(2,92)1/2=1,7;
sNPV=((-1,96-7,262)2× 0,05+(6,8-7,262)2× 0,7+(10,4-7,262)2× 0,25)1/2=
=(6,863)1/2=2,61.
Расчет средних квадратических отклонений вновь подтвердил, что проект Б более рискованный, чем проект А.
Методика изменения денежного потока
В основе данной методики используется полученная экспертным путем вероятностная оценка величины членов ежегодного денежного потока, на основе которой корректируется и рассчитывается значение NPV.
Предпочтение отдается проекту, имеющему наибольшее значение откорректированного NPV; данный проект считается наименее рискованным.
Пример 2. Анализируются два альтернативных проекта А и Б, срок их реализации – 4 года, цена капитала – 12%. Величина необходимых инвестиций составляет для проекта А – 50 млн. руб.; для проекта Б – 55 млн. руб.
Результаты расчетов и денежные потоки приведены в табл. 8.3.3.
По данным таблицы можно сделать вывод: проект Б является более предпочтительным, так как его значение NPV до корректировки и после нее является наибольшим, что свидетельствует не только о выгодности данного проекта, но и обеспечивает наименьший риск при его реализации.
Таблица 8.3.3
(млн. руб.)
| Годы | Проект А | |||||
| Денеж- ный поток | Коэффи- циенты дисконти- рования по ставке 12% | Дисконти- рованные члены потока (гр.2×гр.3) | Экспертная оценка вероятности поступления денежного потока | Откоррек- тированные члены денежного потока (гр.2×гр.5) | Дискконти- рованные члены откоррек- тирован- ного потока (гр.6×гр.3) | |
| 0-й | -50 | -50 | -50 | -50 | ||
| 1-й | 0,893 | 24,111 | 0,9 | 24,30 | 21,7 | |
| 2-й | 0,797 | 21.519 | 0,85 | 22,95 | 18,3 | |
| 3-й | 0,712 | 15,664 | 0,80 | 17,60 | 12,5 | |
| 4-й | 0,636 | 13,992 | 0,75 | 16,50 | 10,5 |
Для проекта А – NPV=25,286, откорректированное NPV=13,00.
Продолжение табл. 8.3.3
| Годы | Проект Б | |||||
| Денеж- ный поток | Коэффи- циенты дисконти- рования по ставке 12% | Дисконти- рованные члены потока (гр.8×гр.3) | Экспертная оценка вероятности поступления денежного потока | Откоррек- тированные члены денежного потока (гр.8×гр.10) | Дискконти- рованные члены откоррек- тирован- ного потока (гр.11×гр.3) | |
| 0-й | -55 | -55 | -55 | -55 | ||
| 1-й | 0,893 | 31,26 | 0,8 | 28,0 | 25,0 | |
| 2-й | 0,797 | 29,49 | 0,75 | 27,75 | 22,12 | |
| 3-й | 0,712 | 26,34 | 0,70 | 25,90 | 18,44 | |
| 4-й | 0,636 | 15,90 | 0,65 | 16,25 | 10,30 |
Для проекта Б – NPV=48,33, откорректированное NPV=20,86.
Поиск по сайту: