 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вопрос 4. Эквивалентность процентных ставок различного типа
.
Эквивалентные процентные ставки – это такие процентные ставки разного вида, применение которых при одинаковых начальных условиях дает одинаковые финансовые результаты. Их необходимо знать в случаях, когда существует возможность выбора условий финансовой операции и требует инструмент для корректного сравнения различных процентных ставок.
Для нахождения эквивалентных процентных ставок используются уравнения эквивалентности, принцип составления которых заключается в выборе величины, которую можно рассчитать при использовании различных процентных ставок (обычно это наращенная сумма S). На основе равенства двух выбранных для данной величины и составляется уравнение эквивалентности, из которого путем соответствующих преобразований получается соотношение, выражающее зависимость между процентными ставками различного вида.
Например. Расчет наращенной суммы по простым процентам осуществляется по формуле S = P (1 + ni), а по учетной ставке - S= P/(1-nd), приравнивая эти соотношения получим:
1 + ni = 1/(1-nd).
В современных условиях проценты могут капитализироваться не один, а несколько раз в году (по дням, неделям, месяцам, кварталам, т.е. m раз). Число раз начисления процентов в году обязательно фиксируется в условиях договора. Кроме того, в контракте оговаривается номинальная ставка процентов j – годовая ставка, исходя из которой, определяется величина ставки, применяемая в каждом периоде начисления. Если проценты начисляют не раз в году, то в каждом периоде применяют ставку j / m, которая представляет собой частное отделения годовой номинальной ставки на число периодов присоединения процентов в году. Так, если годовая ставка 0,06, то при капитализации процентов по полугодиям нужно использовать ставку 0,03, а по кварталам — 0,15. При этом с увеличением процесс наращения суммы ссуды ускоряется.
Расчет наращенной суммы при начислении процентов m раз в году по номинальной ставке производится по следующей формуле:
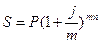 |
где; j — годовая номинальная ставка;
m — число раз присоединения процентов в году;
n — срок ссуды.
Эффективная (или действительная) ставка процентов – это ставка, под которой понимают ту реальную прибыль, которую получают от одной денежной единицы за год. Иначе говоря, эффективная ставка эквивалентна номинальной при начислении процентов m раз в год. Она показывает, какая годовая ставка дает тот же эффект, что и m -разовое наращивание в год по ставке j/m.
 |
Обозначим эффективную ставку через i (эффективная ставка является годовой). Если проценты капитализируются m раз в год, то можно записать следующее равенство:
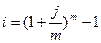 |
Решив это равенство относительно i, получим:
Итак, имея ввиду что эффективная ставка (i) определяется на основании номинальной ставки (j) эта формула рассматривается как формула расчета эффективной ставки.
Учитывая то, что с помощью эффективной ставки обычно изменяется доходность финансовой операции, рассчитанные выше эффективные ставки будут представлять собойреальные доходности вкладов при различных периодах начисления процентов.
Поиск по сайту: