Правила сложения для Д4 кодов

Рассмотрим таблицу возможных значений выходов ДДС для Д4 кода (табл.3). Анализ таблицы показывает что при сложении чисел в Д4 коде могут возникнуть следующие случаи:

1. Если С_i 15 (перенос отсутствует) то необходимо ввести коррекцию -3₁₀(-0011₂),+13₁₀(+1101₂), без формирования переноса.

Табл. 3.

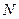
	P4	S*4 S*3 S*2 S*1	Ci	Ci11
		0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1	A B C D E F	- - - - - -	I   II С111 = С* - 3   III   IV   V С112 = С* + 3   VI
	0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1	A B C D E F	- - - - - -

2. Если С_i 16 (перенос возникает) то необходимо

ввести коррекцию +3₁₀(0011₂), здесь С_i - сумма в двоичном коде.

Действительно в первом случае при сложении двух чисел в Д4 коде получаем:

С₁^*_i = А_i +B_i+P_i-1+3+3

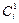
Откуда: = -3 есть истинная сумма в Д4 коде, так как отсутствует перенос P_i.

Где: 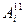= A_i+3, 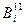= B_i+3, = C_i+3.

C₁*_i- двоичная сумма слагаемых представленных в Д4 коде при отсутствии переноса.

Во втором случае (при возникновении переноса P_i) получаем:

С₂^*_i = А_i +B_i+P_i-1+3+3

C_i

Таким образом во втором случае (т.е. при возникновении переноса P_i=16 единицам) получаем число

С₂^*_i = А_i +B_i+P_i-1+3+3

которое состоит из переноса P_i=16 и суммы по модулю 16.

Следовательно:

S^*_i = А_i +B_i+P_i-1+3+3-16= А_i +B_i+P_i-1-10

C_i

Где: - S^* сумма по модулю.

- 10 перенос для двоично-десятичного кода.

Таким образом сформировалась сумма S^*_i без избытка 3, т.е. в ней не хватает числа 3, чтобы быть Д4 кодом. Следовательно к содержимому сумматора необходимо прибавить +3₁₀(0011)₂.

Схема сумматора Д4 кода приведена на рис.3.

Он состоит из двух ступеней. В первой ступени осуществляется суммирование на 4 ^х разрядном сумматоре (SM1…SM4). Во второй ступени вводится коррекция.

Где: II и V – области разрешенных комбинаций,

I, III, IV и VI – области запрещенных комбинаций.

= A_i+3; = B_i+3; =C_i+3.

Рис.3

Где S^* (S₄^* S₃^* S₂^* S₁^*)- сумма по модулю 16.

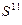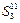
( )- сумма по модулю в коде Д4.

.

2.2.4. Принцип построения сумматора для кода8421+∆ (общий случай).

Обозначим:

1. A^∆_i=A_i + ∆

B^∆_i=B_i + ∆

C^∆_i=C_i + ∆ [C^∆_i =(A_i + ∆)+(B_i + ∆)+ P_i-1 - ∆]= A_i + B_i + P_i-1+ ∆

где A_i,B_i, C_i - числа в коде 8421.

2. S ¹_i = (S¹₁, S¹₂, S¹₃, S¹₄) – значение суммы на выходах S первой ступени сумматора (SM₁..SM_n) в двоичной системе счисления,

C ¹_i = (P₄, S ¹_i) – полная сумма (в двоичной системе счисления на всех выходах первой ступени SM.

3. S ² _i = (S²₁, S²₂, S²₃, S²₄) – значение суммы на выходах S второй ступени сумматора (SM_n+1..SM_2n) по модулю заданной системы счисления;

C ²_i = (P_i(n), S ²_i) – полная истинная сумма на выходе второй ступени сумматора в заданном коде и заданной системе счисления.

Где:

P_i(n) – перенос в старший разряд, количественный эквивалент которого равен q_i(n)+ ∆,

q_i(n) – основание заданной системы счисления.

Тогда:

1. Если C¹_i = A^∆_i + B^∆_i + P_i-1 < q_i(n)+ 2∆,

то: P_i(n) = 0,

а C²_i = C¹_i - ∆.

Действительно, C ¹_i = A^∆_i + B^∆_i + P_i-1= A_i + B_i + P_i-1+ ∆+∆= C^∆_i+ ∆

2. Если C ¹_i = A^∆_i + B^∆i + P_i-1 ≥ q_i(n)+ 2∆

то: P_i(n) = 1,

а C²_i = C¹_i – [q_i(n)+ ∆]

Где:

[q_i(n)+ ∆] – количественный эквивалент основания системы счисления в заданном коде.

Таким образом:

1. Если сумма на выходе первой ступени сумматора (C¹_i) меньше заданного основания системы счисления q_i(n) плюс 2∆, т.е. [q_i(n)+2∆], то перенос в старший разряд отсутствует – [P_i(n) = 0], а истинная сумма будет формироваться на второй ступени сумматора, путем вычитания из C¹_i значения ∆.

2.Если сумма на выходе первой ступени сумматора C¹_i, больше или равна [q_i(n)+ 2∆], то перенос в старший разряд равен 1, т.е. [P_i(n) = 1], а из суммы C¹_i на второй ступени вычитается основание системы счисления в заданном коде [q_i(n)+ ∆]

Примечание:

1. На выходе первой ступени сумматора сумма C ¹_i получается в двоичной системе счисления.

2. На выходе второй ступени сумматора сумма C ²_i является истинной суммой в заданном коде.

3. Операция вычитания величин ∆ и [q_i(n)+ ∆] осуществляется на второй ступени сумматора, путем сложения с дополнительными кодами соответствующих величин “ ∆” и [ q_i(n)+ ∆ ].

Пример:

A_i=7, B_i=8, =5, q_i(10), т.е. код 8421+5 и основание системы счисления равно 10.

Тогда:

A _i=7+5=12(1100), B _i =8+5=13(1101),