 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Концепция и методический инструментарий оценки стоимости денег во времени
Концепция стоимости денег во времени состоит в том, что стоимость денег с течением времени изменяется с учетом нормы прибыли на финансовом рынке, в качестве которой обычно выступает норма ссудного процента (или процента).
Иными словами, в соответствии с этой концепцией одна и та же сумма денег в разные периоды времени имеет разную стоимость, эта стоимость в настоящее время всегда выше, чем в любом будущем периоде.
Базовые понятия, используемые при оценке стоимости денег с учетом фактора времени.
| ПРОЦЕНТ – | сумма дохода от предоставления капитала в долг или плата за пользование ссудным капиталом во всех его формах (депозитный процент, кредитный процент, процент по облигациям, процент по векселям и т. п.). |
| ПРОСТОЙ ПРОЦЕНТ – | сумма дохода, начисляемого к основной сумме капитала в каждом интервале, по которой дальнейшие расчеты платежей не осуществляются. Начисление простого процента применяется, как правило, при краткосрочных финансовых операциях. |
| СЛОЖНЫЙ ПРОЦЕНТ – | сумма дохода, начисляемого в каждом интервале, которая не выплачивается, а присоединяется к основной сумме капитала и в последующем платежной периоде сама приносит доход. Применяется, как правило, при долгосрочных финансовых операциях. |
| ПРОЦЕНТНАЯ СТАВКА – | удельный показатель, в соответствии с которым в установленные сроки выплачивается сумма процента в расчете на единицу капитала. Обычно процентная ставка характеризует соотношение годовой суммы процента и суммы предоставленного (заимствованного) капитала (выраженное в десятичной дроби или в процентах). |
| БУДУЩАЯ СТОИМОСТЬ ДЕНЕГ – | сумма инвестированных в настоящий момент денежных средств, в которую они превратятся через определенный период времени с учетом определенной ставки процента (процентной ставки). |
| НАСТОЯЩАЯ СТОИМОСТЬ ДЕНЕГ – | сумма будущих денежных средств, приведенных с учетом определенной ставки процента (процентной ставки) к настоящему периоду времени. |
| НАРАЩЕНИЕ СТОИМОСТИ (компаундинг) – | процесс приведения настоящей стоимости денег к их будущей стоимости в определенном периоде путем присоединения к их первоначальной сумме начисленной суммы процентов. |
| ДИСКОНТИРОВАНИЕ СТОИМОСТИ – | процесс приведения будущей стоимости денег к их настоящей стоимости путем изъятия из их будущей суммы соответствующей суммы процентов (называемой «дисконтом»). |
| ПЕРИОД НАЧИСЛЕНИЯ – | общий период времени, в течение которого осуществляется процесс наращения или дисконтирования стоимости денежных средств. |
| ИНТЕРВАЛ НАЧИСЛЕНИЯ – | обусловленный конкретный временной срок (в пределах общего периода начисления), в рамках которого рассчитывается отдельная сумма процента по установленного его ставке (осуществляется отдельный платеж процента). |
| ПРЕДВАРИТЕЛЬНЫЙ МЕТОД НАЧИСЛЕНИЯ ПРОЦЕНТА – | (метод пренумерандо или антисипативный метод) – способ расчета платежей, при котором начисление процента осуществляется в начале каждого интервала. |
| ПОСЛЕДУЮЩИЙ МЕТОД НАЧИСЛЕНИЯ ПРОЦЕНТА – | (метод постнумерандо или декурсивный метод) – способ расчета платежей, при котором начисление процента осуществляется в конце каждого интервала. |
| ДИСКРЕТНЫЙ ДЕНЕЖНЫЙ ПОТОК – | поток платежей на вложенный капитал, имеющий четко ограниченный период начисления процентов и конечный срок возврата основной его суммы. |
| НЕПРЕРЫВНЫЙ ДЕНЕЖНЫЙ ПОТОК – | поток платежей на вложенный капитал, период начисления процентов по которому не ограничен, а соответственно не определен и конечный срок возврата основной суммы долга. |
| АННУИТЕТ (ФИНАНСОВАЯ РЕНТА) – | длительный поток платежей, характеризующийся одинаковым уровнем процентных ставок на протяжении всего периода. |
Классификация видов процентной ставки
1. По использованию в процессе форм оценки стоимости денег во времени:
– ставка наращения;
– ставка дисконтирования (дисконтная ставка).
2. По стабильности уровня используемой процентной ставки в рамках периода начисления:
– фиксированная процентная ставка;
– плавающая (переменная) процентная ставка.
3. По обеспечению начисления определенной годовой суммы процента:
– периодическая ставка процента;
– эффективная ставка процента (или ставка сравнения);
4. По условиям формирования:
– базовая процентная ставка;
– договорная процентная ставка.
1. По использованию в процессе форм оценки стоимости денег во времени различают
а) ставка наращения представляет собой процентную ставку, по которой осуществляется процесс наращения стоимости денежных средств (компаундинг), т. е. Определяется их будущая стоимость.
б) ставка дисконтирования (дисконтная ставка) представляет собой процнтную ставку, по которой осуществляется процесс дисконтирования стоимости денежных средств, т. е. определяется их настоящая стоимость.
2. По стабильности уровня используемой процентной ставки в рамках периода начисления:
а) фиксированная процентная ставка характеризуется неизменным ее уровнем на протяжении всех интервалов общего периода начисления;
б) плавающая (переменная) процентная ставка характеризуется регулярно пересматриваемым ее уровнем по соглашению сторон в разрезе отдельных интервалов общего периода начислений. Такой пересмотр обусловливается изменением средней нормы процента на финансовом рынке, изменением темпа инфляции и другими условиями.
3. По обеспечению начисления определенной годовой суммы процента:
а) периодическая ставка процента при обеспечении определенной годовой суммы процента может варьироваться как по уровню, так и по продолжительности отдельных интервалов на протяжении годового периода платежей.
б) эффективная ставка процента (или ставка сравнения) характеризует среднегодовой ее уровень, определяемый отношением годовой суммы процента, начисленного по периодическим его ставкам, к основной сумме капитала.
4. По условиям формирования:
а) базовая процентная ставка характеризуется определенным исходным ее уровнем в качестве первоначальной основы последующей ее конкретизации кредитором (заемщиком) в зависимости от условий осуществления соответствующей финансовой операции;
б) договорная процентная ставка характеризует конкретизированный ее уровень, согласованный кредитором и заемщиком и отраженный в соответствующем кредитном (депозитном, инвестиционном) договоре.
I. МЕТОДИЧЕСКИЙ ИНСТРУМЕНТАРИЙ ОЦЕНКИ СТОИМОСТИ ДЕНЕГ ПО ПРОСТЫМ ПРОЦЕНТАМ
Использует наиболее упрощенную систему расчетных алгоритмов.
1. При расчете суммы простого процента в процессе наращения стоимости (компаудинга) используется формула:
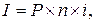(1)
где I – сумма процента за обусловленный период времени в целом; Р – первоначальная сумма (стоимость) денежных средств; n – количество интервалов, по которым осуществляется расчет процентных платежей, в общем обусловленном периоде времени; i – используемая процентная ставка, выраженная десятичной дробью.
В этом случае будущая стоимость вклада (S) с учетом начисленной суммы процента определяется по формуле:
(2)
Множитель 
, называется коэффициентом наращения суммы простых процентов. Коэффициент наращения суммы простых процентов всегда должен быть больше 1.
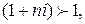(3)
2. При расчете суммы простого процента в процессе дисконтирования стоимости (т. Е. суммы дисконта) используется следующая формула:
(4)
где D – сумма дисконта (рассчитанная по простым процентам) за обусловленный период времени в целом; S – стоимость денежных средств; n – количество интервалов, по которым осуществляется расчет процентных платежей, в общем обусловленном периоде времени; i – используемая процентная ставка, выраженная десятичной дробью.
В этом случае, настоящая стоимость денежных средств (Р) с учетом рассчитанной суммы дисконта определяется по формуле:
(5)
Множитель 
называется дисконтным коэффициентом суммы простых процентов, значение которого всегда должно быть меньше 1.
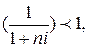(6)
II. МЕТОДИЧЕСКИЙ ИНСТРУМЕНТАРИЙ ОЦЕНКИ СТОИМОСТИ ДЕНЕГ ПО СЛОЖНЫМ ПРОЦЕНТАМ
1. При расчете будущей стоимости вклада (стоимости денежных средств) в процессе его наращения по сложным процентам используется формула:
(7)
Где Sc – будущая стоимость вклада (денежных средств) при его наращении по сложным процентам; Р – первоначальная стоимость вклада; n – количество интервалов, по которым осуществляется расчет процентных платежей, в общем обусловленном периоде времени; i – используемая процентная ставка, выраженная десятичной дробью.
Соответственно, сумма процента (Ic) определяется по формуле:
(8)
2. При расчете настоящей стоимости денежных средств в процессе дисконтирования по сложным процентам используется формула:
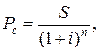(9)
где Рс – первоначальная сумма вклада; S – будущая стоимость вклада при его наращении, обусловленная условиями инвестирования.
Соответственно сумма дисконта (Dc) в этом случае определяется по формула:
(10)
3. При определении средней процентной ставки, используемой в расчетах стоимости денежных средств по сложным процентам, применяется формула:
(11)
4. Длительность общего периода платежей, выраженная количеством его интервалов, в расчетах стоимости денежных средств по сложным процентам определяется путем логарифмирования по формуле:
(12)
где Sc – будущая стоимость денежных средств; Рс – первоначальная сумма денежных средств; i – используемая процентная ставка, выраженная десятичной дробью.
5. Определение эффективной процентной ставки в процессе наращениястоимости денежных средств по сложным процентам осуществляется по формуле:
(13)
При оценке стоимости денег во времени по сложным процентам необходимо иметь в виду, что на результат оценки оказывает большое влияние не только используемая ставка процента, но и число интервалов выплат в течение одного и того же общего платежного периода. Иногда оказывается более выгодным инвестировать деньги под меньшую ставку процента, но с большим числом интервалов в течение предусмотренного периода платежа.
III. МЕТОДИЧЕСКИЙ ИНСТРУМЕНТАРИЙ ОЦЕНКИ СТОИМОСТИ ДЕНЕГ ПРИ АННУИТЕТЕ
Связан с использованием наиболее сложных алгоритмов и определением метода начисления процента – предварительным (пренумерандо) или последующим (постнумерандо).
1. При расчете будущей стоимости аннуитета на условиях предварительных платежей (пренумерандо) используется формула:
(14)
где 
– будущая стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо); R – член аннуитета, характеризующий размер отдельного платежа; n – количество интервалов, по которым осуществляется расчет процентных платежей, в общем обусловленном периоде времени; i – используемая процентная ставка, выраженная десятичной дробью.
2. При расчете будущей стоимости аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), применяется формула:
(15)
где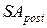 
– будущая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо).
3. При расчете настоящей стоимости аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо) используется формула:
(16)
де 
– настоящая стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо).
4. При расчете настоящей стоимости аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), применяется формула:
(17)
где 
– настоящая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо).
5. При расчете размера отдельного платежа при заданной будущей стоимости аннуитета используется формула:
(18)
R – размер отдельного платежа по аннуитету (член аннуитета при предопределенной будущей его стоимости).
6. При расчете размера отдельного платежа при заданной текущей стоимости аннуитета используется формула:
(19)
R – размер отдельного платежа по аннуитету (член аннуитета при известной текущей его стоимости).
В процессе расчета аннуитета возможно использование упрощенных формул, основу которых составляет только член аннуитета (размер отдельного платежа) и соответствующий стандартный множитель (коэффициент) его наращения или дисконтирования.
В этом случае формула для определения будущей стоимости аннуитета (осуществляемого на условиях последующих платежей), имеет вид:
(20)
где 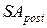– будущая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо).
Соответственно, формула для определения настоящей стоимости аннуитета имеет вид:
(21)
– настоящая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо).
В специальных приложениях финансового менеджмента приведены множители наращения стоимости аннуитета и его дисконтные множители.
Поиск по сайту: