Мера риска для одиночного актива

Наиболее популярный метод анализа инвестиционных рисков основан на использовании математического ожидания в качестве индикатора ожидаемого инвестором дохода (доходности) на инвестицию и дисперсии либо стандартного отклонения в качестве меры риска.

Ожидаемый доход1 Ř определяется как средневзвешенное значение возможных исходов R_i, где весами служат вероятности наступления конкретных исходов p_i:

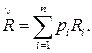(3.3)

Дисперсия σ² определяется соотношением:

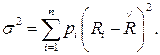(3.4)

Стандартное отклонение определится как квадратный корень из дисперсии:

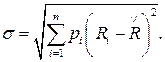(3.5)

По своему смыслу дисперсия и стандартное отклонение представляют собой меру разброса возможных исходов относительно средней (ожидаемой) величины. В соответствии с приведенным выше определением финансового риска, чем выше значение любой из этих величин, тем выше риск. В качестве меры риска стандартное отклонение используется все же чаще, в силу того соображения, что она имеет размерность денежной единицы, в то время как дисперсия – денежной единицы в квадрате, что с экономической точки зрения бессмысленно.

Кроме описанных выше, может быть использован и такой статистический показатель риска, как коэффициент вариации. Последний может быть определен как отношение стандартного отклонения к ожидаемому доходу:

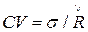(3.6)

Поиск по сайту: