 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
КОНТРОЛЬНАЯ РАБОТА №1. 1. Решить систему линейных уравнений методом Гаусса
1. Решить систему линейных уравнений методом Гаусса.
1.1.  1.2.
1.2. 
1.3.  1.4.
1.4. 
1.5.  1.6.
1.6. 
17.  1.8.
1.8. 
19.  1.10.
1.10. 
1.11.  1. 12.
1. 12. 
1.13.  1.14.
1.14. 
1.15.  1.16.
1.16. 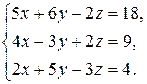
1.17. 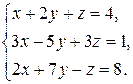 1.18.
1.18. 
1.19.  1.20.
1.20. 
2. Определить тип кривой, найти ее параметры; определить угловой коэффициент прямой. Найти точки пересечения данных линий и сделать чертеж.
2.1.  ;
;  .
.
2.2. 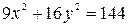 ;
;  .
.
2.3.  ;
;  .
.
2.4. 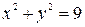 ;
;  .
.
2.5.  ;
;  .
.
2.6.  ;
; 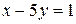 .
.
2.7. 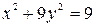 ;
;  .
.
2.8. 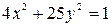 ;
;  .
.
2.9.  ;
; 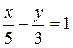 .
.
2.10.  ;
;  .
.
2.11.  ;
;  .
.
2.12.  ;
;  .
.
2.13. 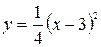 ;
;  .
.
2.14. 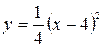 ;
;  .
.
2.15.  ;
;  .
.
2.16.  ;
;  .
.
2.17.  ;
;  .
.
2.18.  ;
; 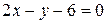 .
.
2.19.  ;
;  .
.
2.20.  ;
;  .
.
3. Даны координаты вершин пирамиды АВСD. Требуется:
1) записать векторы  в системе орт
в системе орт  и найти модули этих векторов;
и найти модули этих векторов;
2) найти угол между векторами  и
и 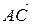 ;
;
3) найти проекцию вектора 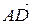 на вектор
на вектор  ;
;
4) найти площадь грани АВС;
5) найти объем пирамиды АВСD;
6) составить уравнение ребра АС;
7) составить уравнение грани АВС.
3.1. 
3.2. 
3.3. 
3.4. 
3.5. 
3.6. 
3.7. 
3.8. 
3.9. 
3.10. 
3.11. 
3.12. 
3.13. 
3.14. 
3.15. 
3.16. 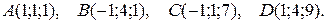
3.17. 
3.18. 
3.19. 
3.20. 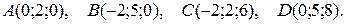
4. Провести полное исследование функции методами дифференциального исчисления и построить ее график.
41.  . 4.2.
. 4.2.  .
.
4.3.  . 4.4.
. 4.4. 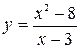 .
.
4.5.  . 4.6.
. 4.6.  .
.
4.7.  . 4.8.
. 4.8. 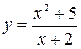 .
.
4.9.  . 4.10.
. 4.10.  .
.
4.11.  . 4.12.
. 4.12.  .
.
4.13.  . 4.14.
. 4.14.  .
.
4.15.  . 4.16.
. 4.16.  .
.
4.17.  . 4.18.
. 4.18.  .
.
4.19.  . 4.20.
. 4.20.  .
.
5. Решить систему двух линейных уравнений в области комплексных чисел по формулам Крамера. Найденные  изобразить на комплексной плоскости в виде векторов и записать их в показательной и тригонометрической формах.
изобразить на комплексной плоскости в виде векторов и записать их в показательной и тригонометрической формах.
5.1.  5.2.
5.2. 
5.3. 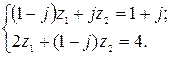 5.4.
5.4. 
5.5.  5.6.
5.6. 
5.7.  5.8.
5.8. 
5.9. 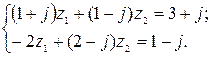 5.10.
5.10. 
5.11.  5.12.
5.12. 
5.13.  5.14.
5.14. 
5.15.  5.16.
5.16. 
5.17. 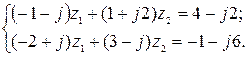 5.18.
5.18. 
5.19.  5.20.
5.20. 
6. а) Вычислить площадь фигуры, расположенной в первом квадранте и ограниченной параболой, прямой и осью Ox.
б) Найти объем тела, образованного вращением этой фигуры вокруг оси Ох.
6.1.  .
.
6.2.  .
.
6.3.  .
.
6.4.  .
.
6.5.  .
.
6.6  .
.
6.7.  .
.
6.8. 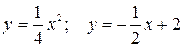 .
.
6.9.  .
.
6.10.  .
.
6.11  .
.
6.12.  .
.
6.13  .
.
6.14.  .
.
6.15.  .
.
6.16 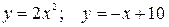 .
.
6.17  .
.
6.18.  .
.
6.19.  .
.
6.20. 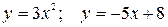 .
.
Поиск по сайту: