 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Решение. Изобразим пластинку на плоскости xOy
Изобразим пластинку на плоскости xOy.
 у
у
 В
В
 0 А х
0 А х
Масса неоднородной пластинки выражается через двойной интеграл по формуле:  .
.
В нашем случае область D - треугольник ОАВ,  .
.
Запишем уравнение прямой АВ, используя уравнение прямой в отрезках:
 , откуда получаем
, откуда получаем  ; область D задаётся как решение системы неравенств
; область D задаётся как решение системы неравенств 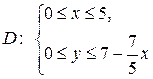
Вычислим массу m, переходя от двойного к повторному интегралу:




12. а) (Только для профиля ТСА.)Вычислить работу, совершаемую переменной силой  по прямой, соединяющей точки М (1; 1) и N (2; 3).
по прямой, соединяющей точки М (1; 1) и N (2; 3).
б) (Только для профилей ЭОЭТ и ЭОП.) Проверить, что векторное поле  потенциально; найти потенциал поля и работу, совершаемую силой
потенциально; найти потенциал поля и работу, совершаемую силой  при переходе из точки М (1; 2) в точку N (3; 5).
при переходе из точки М (1; 2) в точку N (3; 5).
Решение. а) Для того чтобы найти работу, совершаемую переменной силой  , вычислим криволинейный интеграл
, вычислим криволинейный интеграл
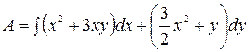
по прямой, соединяющей точки М (1; 1) и N (2; 3).
Запишем уравнение прямой, проходящей через две данные точки:
 .
.
После преобразований получаем:  , поэтому
, поэтому 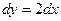 .
.
Перейдем от криволинейного интеграла к определенному, подставляя полученные нами выражения для y и dy и учитывая, что  .
.
Тогда работа A примет вид

 у
у
N
 3
3
1 M
 |
0 1 2 х
б) Векторное поле имеет вид  . Поэтому
. Поэтому
 ,
,  . Найдем частные производные
. Найдем частные производные  .
.
Производные совпадают, откуда следует, что поле  потенциально.
потенциально.
Потенциал векторного поля  находим по формуле
находим по формуле
 .
.
Для нашего случая
 ,
,
то есть потенциал данного поля равен
 .
.
Проверим, правильно ли мы нашли потенциальную функцию. Для этого должны выполняться следующие условия:
 .
.
В нашем случае:
 по условию
по условию  ,
,
 по условию
по условию  .
.
В потенциальных полях работа A силы  равна разности потенциалов, то есть
равна разности потенциалов, то есть 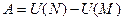 .
.
В нашем случае
 .
.
13. Найти вероятность безотказной работы участка цепи, если известно, что каждый  -ый элемент работает независимо от других с вероятностью
-ый элемент работает независимо от других с вероятностью 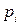 (
( = 1, 2, 3, 4, 5, 6).
= 1, 2, 3, 4, 5, 6).  .
.
 |
Решение. Участок цепи будет работать безотказно, если работают блоки 1–2 и 3–4–5–6 (последовательное соединение).
Рассмотрим блок 1–2. Элементы 1 и 2 соединены параллельно, следовательно, блок 1–2 будет работать, если хотя бы один из элементов 1, 2 исправен.
 – надежность блока 1–2.
– надежность блока 1–2.
Рассмотрим блок 3–4–5–6. Блок 3–4–5–6 будет безотказно работать хотя бы в одном из случаев:
исправны элементы 3 и 4,
исправен элемент 5,
исправен элемент 6.
 – вероятность безотказной работы блока 3–4.
– вероятность безотказной работы блока 3–4.
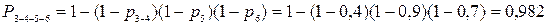 –
–
надежность блока 3–4–5–6.
Следовательно,
 – искомая надежность участка цепи.
– искомая надежность участка цепи.
14. Измерены диаметры  для 90 деталей, обрабатываемых на некотором станке. Данные замеров приведены в табл. 1.
для 90 деталей, обрабатываемых на некотором станке. Данные замеров приведены в табл. 1.
Таблица 1
| 70,88 | 67,04 | 69,20 | 66,24 | 64,80 | 71,52 | 67,52 | 68,96 | 67,36 | 68,64 |
| 67,12 | 66,96 | 69,04 | 66,00 | 66,00 | 64,88 | 65,84 | 67,52 | 65,68 | 70,00 |
| 70,80 | 66,32 | 67,40 | 66,08 | 69,76 | 68,01 | 65,76 | 69,20 | 65,60 | 66,72 |
| 67,44 | 67,72 | 68,72 | 64,00 | 66,32 | 68,21 | 70,96 | 67,76 | 66,88 | 69,12 |
| 65,84 | 64,88 | 69,46 | 68,48 | 65,04 | 70,00 | 70,16 | 68,72 | 67,04 | 69,36 |
| 66,48 | 68,20 | 64,72 | 70,40 | 67,76 | 69,28 | 71,20 | 67,90 | 66,80 | 70,24 |
| 69,15 | 67,68 | 69,36 | 67.46 | 65,48 | 66,98 | 71,40 | 68,15 | 68,88 | 65,26 |
| 64,71 | 68,36 | 67,13 | 66,18 | 68,19 | 67,05 | 68,90 | 68,72 | 69,21 | 68,14 |
| 66,99 | 64,44 | 68,05 | 69,40 | 70,01 | 68,76 | 67,70 | 70,00 | 71,32 | 70,46 |
Выполнить статистическую обработку результатов измерений по следующему плану.
1) Построить вариационный ряд.
2) Найти точечные оценки математического ожидания (генеральной средней 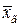 ) и дисперсии
) и дисперсии  случайной величины (признака)
случайной величины (признака)  .
.
3) Построить гистограмму относительных частот.
4) На том же чертеже построить кривую нормального распределения и провести анализ соответствия выборочных данных нормальному закону распределения случайной величины Х.
Поиск по сайту: