КОНТРОЛЬНАЯ РАБОТА №2. 7.Классическим методом найти частное решение системы дифференциальных уравнений удовлетворяющее начальным условиям

7. Классическим методом найти частное решение системы дифференциальных уравнений 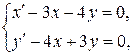удовлетворяющее начальным условиям .

Решение. Решением этой системы является пара функций , , удовлетворяющих системе, причем .

Продифференцируем первое уравнение по переменной :

.

Из первого уравнения определяем , следовательно, из второго уравнения имеем

.

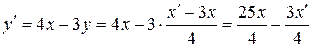Подставляем в уравнение, полученное после дифференцирования, приходим к уравнению

,

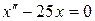– линейное дифференциальное уравнение II порядка с

постоянными коэффициентами.

Составляем характеристическое уравнение и находим его корни:

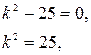
– действительные различные корни.

В этом случае общее решение дифференциального уравнения имеет вид

,

.

Ранее определили . Тогда

.

Общее решение системы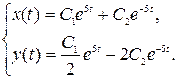

Находим значения произвольных постоянных, используя начальные условия :

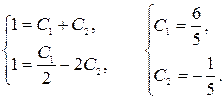
Частное решение системы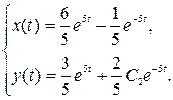

8. Вычислить определённый интервал с точностью до 0,001 путём разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.

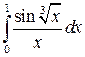
Поиск по сайту: