КОНТРОЛЬНАЯ РАБОТА №1. 1. Решить систему линейных уравнений методом Гаусса

1. Решить систему линейных уравнений методом Гаусса.

Решение. Первое уравнение умножается на (-2) и прибавляется ко второму уравнению, затем первое уравнение умножается на (-3) и прибавляется к третьему. Таким образом, неизвестное х исключается из двух последних уравнений. Эти преобразования лучше показать на расширенной матрице

.

Вычтя во второй матрице из третьей строки удвоенную вторую, мы исключаем неизвестное у из третьего уравнения. После таких преобразований получается система

Из третьего уравнение легко находится . Затем из второго уравнения получаем . Наконец, из третьего уравнения получаем .

Нетрудно проверить, что совокупность , , 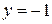является решением данной системы.

2. Определить тип кривой , найти ее параметры; определить угловой коэффициент прямой 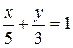. Найти точки пересечения данных линий и сделать чертеж.

Решение. Приведем уравнение кривой к каноническому виду , разделив на 225. Получим уравнение эллипса 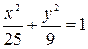. Его большая полуось , малая полуось . Центр совпадает с началом координат.

Уравнение прямой 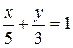имеет вид «в отрезках» , что удобно для построения. Для нахождения углового коэффициента прямой приведем ее к виду , выразим у через х: .

Угловой коэффициент .

Для нахождения точек пересечения этих линий решим систему

Возведем второе уравнение в квадрат

и подставим в первое уравнение:

Нашли точки пересечения (0; 3) и (5; 0), что наглядно видно на чертеже.

у

–5 0 5 х

-3

3. Даны координаты вершин пирамиды АВСD:

Требуется:

1) записать векторы в системе орт и найти модули этих векторов;

2) найти угол между векторами и ;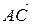

3) найти проекцию вектора 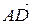на вектор ;

4) найти площадь грани АВС;

5) найти объем пирамиды АВСD;

6) составить уравнение ребра АС;

7) составить уравнение грани АВС.

Поиск по сайту: