Расчет зубьев на прочность при изгибе

Условие прочностной надежности зуба:

(1.20)

где –максимальное напряжение в опасном сечении зуба; – допускаемое напряжение изгиба для материала зуба.

Для оценки прочностной надежности зубчатой передачи необхо­димо иметь уравнение, связывающее максимальные напряжения в опас­ном сечении с внешней нагрузкой на зуб и размерами опасного сече­ния (параметрами передачи).

а). Прямозубые цилиндрические передачи

Расчет выполняют для наиболее опасного случая – однопарного зацепления, когда вся внешняя нагрузка передается одной парой зубьев.

(1.21)

где F_t – окружная сила; B_W –ширина венца колеса; m –модуль зацепления; y_F – коэффициент формы зуба; K_Fα – коэффициент, учитывающий одновременное участие в передаче нагрузки нескольких пар зубьев (K_Fα= 1); K_Fβ –коэффициент концентрации нагрузки; K_Fυ –коэффициент динамической нагрузки.

б). Косозубые цилиндрические передачи

(1.22)

где – коэффициент, учитывающий наклон зубьев; –коэффициент перекрытия; где – коэффици­ент ширины колеса; для колес низкой твердости (не более 350 НВ); (более 350 НВ).

Ширину зубчатых колес принимают в зависимости от диаметра шестерни.

в). Конические передачи

В опасном сечении зуба конического колеса максимальные напря­жения

(1.23)

где – экспериментальный коэффициент, учитывающий пониженную нагрузочную способность конических передач по сравнению с цилинд­рическими передачами из-за конструктивных особенностей; m –мо­дуль в среднем нормальном сечении зуба.

= 0,85 – для конических прямозубых передач;

1-1.2 – для передач с круговыми зубьями.

2. Расчет на контактную прочность активных поверхностей зубьев

Расчет зубьев выполняют для фазы зацепления в полюсе.

(1.24)

где –максимальное контактное напряжение на активной поверх­ности зубьев; 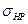–допускаемое контактное напряжение.

Контактные напряжения одинаковы для обоих колес, поэтому расчет выполняют для того колеса, у которого 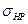меньше.

Для расчета зубчатой передачи на контактную прочность необ­ходимо иметь уравнение, связывающее максимальное напряжение с внешней нагрузкой и параметрами передачи.

а). Прямозубые и косозубые передачи

(1.25)

где Z_H –коэффициент, учитывающий форму сопряженных поверхнос­тей; Z_M–коэффициент, учитывающий механические свойства матери­алов колес (модули упругости Е₁ и Е₂ и коэффициенты Пуассона, и ). Z_M= 275 – для стальных колес; Z_ε – коэффициент, учитыва­ющий суммарную.длину контактных линий.

– для прямозубых передач.

(1.26)

– для косозубых передач.

в предварительных расчетах, –из таблиц. 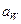–межосевое расстояние; 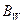–ширина колеса; U – передаточ­ное число.

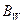принимают в зависимости от межосевого расстояния.

(1.27)

где – коэффициент ширины колеса.

= 0,315-0,5 – при симметричном положении колес;

= 0,25-0,4 – при несимметричном;

= 0,2-0,25 – при консольном расположении.

б). Конические передачи (прямозубые)

Расчет производить по формуле (1.23), где вместо коэффициен­та подставить коэффициент (установлен экспериментально, учитывает особенности прочности конических передач). 0,85 –для прямозубых.

Поиск по сайту: