 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Резонансы
4.1.1. Резонанс напряжений
Общие условия возникновения – равенство нулю реактивного сопротивления цепи.
Резонанс напряжений может возникать в цепях с последовательным соединением участков, содержащих индуктивности и ёмкости.
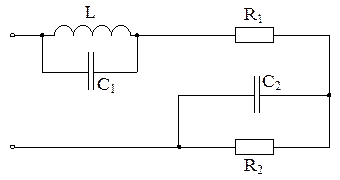 |
Рис.83
 |
Рассмотрим частный случай:
Рис.84
Частотные характеристики участка LC.


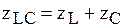 .
.
Рис.85 а Рис.85 б
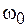 – резонансная частота.
– резонансная частота.
В области частот ниже резонансной цепь имеет ёмкостный характер, в области частот выше резонансной цепь имеет индуктивный характер.
Входное сопротивление всей цепи:
 . (4.5)
. (4.5)
В режиме резонанса:
 . (4.6)
. (4.6)
– условия возникновения резонанса в данной цепи.
Резонанса можно достичь, изменяя частоту, индуктивность или ёмкость.
 . (4.7)
. (4.7)
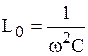 . (4.8)
. (4.8)
 . (4.9)
. (4.9)
В режиме резонанса входное сопротивление цепи  - минимально, а ток - максимален. Сопротивление реактивных элементов на резонансной частоте:
- минимально, а ток - максимален. Сопротивление реактивных элементов на резонансной частоте:
 (4.10)
(4.10)
– называется характеристическим (волновым) сопротивлением контура.
Если в режиме резонанса  , то напряжение на L и C больше входного.
, то напряжение на L и C больше входного.
Отношение
 (4.11)
(4.11)
– называют добротностью контура (показывает: во сколько раз напряжение на катушке больше входного или ток на конденсаторе больше входного в режиме резонанса).
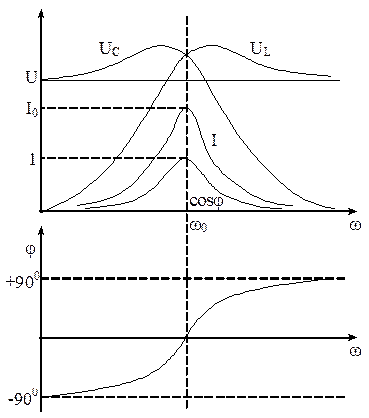 |
Частотные характеристики:
Рис.86
Чем больше величина добротности Q, тем острее резонансные кривые.
Полоса частот вблизи резонансной, на границах которой ток снижается в  раз от своего максимального значения, называется полосой пропускания контура.
раз от своего максимального значения, называется полосой пропускания контура.
При токе  активная мощность, поглощаемая цепью:
активная мощность, поглощаемая цепью:
 (4.12)
(4.12)
составляет половину мощности в режиме резонанса, поэтому полосу пропускания контура характеризуют как полосу, границы которой соответствуют половине резонансной мощности.
Кроме того, на границах полосы пропускания выполняется  . Это следует из:
. Это следует из:
 . (4.13)
. (4.13)
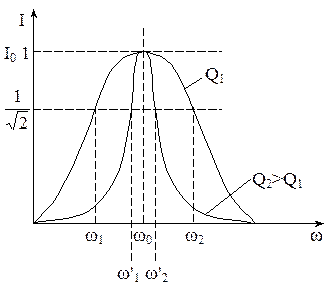 |
На нижней границе полосы пропускания
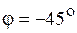 , на верхней
, на верхней  .
.
Рис.87
 |
Рис.88
4.1.2. Резонанс токов
Общее условие возникновения: равенство нулю входной проводимости цепи. Может возникать с параллельным соединением участков содержащих индуктивности и ёмкости.
 |
Рис.89
Рассмотрим частный случай:

 |
Рис.91
 .
.
Рис.90
 |
Частотные характеристики участка LC:
Рис.92 Рис.93
Входная проводимость цепи.
 . (4.14)
. (4.14)
В режиме резонанса:  .
.
Резонанс можно обеспечить, изменяя ёмкость, индуктивность или частоту. Для данной цепи:  ,
, 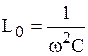 ,
,  .
.
В режиме резонанса входная проводимость цепи  минимальна и ток так же минимален.
минимальна и ток так же минимален.
Проводимости реактивных элементов на резонансной частоте.
 (4.15)
(4.15)
– называются волновой проводимостью контура.
Если в режиме резонанса  , то ток в индуктивности и ёмкости больше входного тока.
, то ток в индуктивности и ёмкости больше входного тока.
Отношение
 (4.16)
(4.16)
– называется добротностью параллельного контура (отражает отношение токов).
 |
Частотные характеристики:
Рис.94
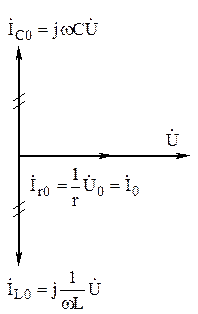 |
Возьмём пример с реальной катушкой.
Рис.95
 |
 . (4.17)
. (4.17)
Умножим и разделим на комплексно сопряжённый знаменатель.
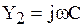 ,
,
 . (4.18)
. (4.18)
В режиме резонанса токов входная проводимость равна нулю, следовательно:
 . (4.19)
. (4.19)
 . (4.20)
. (4.20)
 . (4.21)
. (4.21)
 ,
,  . (4.22)
. (4.22)
Отсюда видно что:
 ,
,  . (4.23)
. (4.23)

Рис.96
Поиск по сайту: