Закон Ома и Кирхгофа в комплексной форме записи

Дано: ,

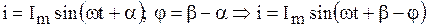. (2.52)

Найти: .

. (2.53)

Поставим в соответствии синусоидальным функциям - комплексные.

. (2.54)

. (2.55)

Сложение, дифференцирование и интегрирование синусоидальных функций в уравнении (2.53) заменим теми же операциями над мнимыми частями комплексных функций.

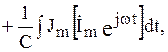(2.56)

Операции дифференцирования и интегрирования мнимых частей ком­плексных функций и операция взятия линейной части взаимопереместимы, поэтому перепишем (2.56) в виде:

. (2.57)

Уравнение (2.57) справедливо для любого момента времени, поэтому вы­ражения в скобках левой и правой части (2.57) равны. Проводя интегрирование и дифференцирование, получим:

, (2.58)

. (2.59)

Обозначим: (2.60)

– комплексное сопротивление сопротивления.

(2.61)

– комплексное сопротивление индуктивности.

(2.62)

– комплексное сопротивление ёмкости.

Тогда: (2.63)

– комплексная амплитуда напряже­ния на сопротивлении.

(2.64)

– комплексная ам­плитуда напряжения на индуктивности.

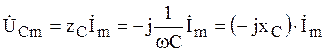(2.65)

– комплексная амплитуда напряжения на ёмкости.

Выражения (2.63, 2.64, 2.65) – закон Ома в комплексной форме записи для от­дельных элементов цепи.

С учетом введенных обозначений:

(2.66)

– второй закон Кирхгофа в комплексной форме записи.

– реактивное сопротив­ление цепи.

. (2.67)

Обозначим: (2.68)

– входное комплексное сопротивление цепи.

– полное сопротив­ление цепи. (2.69)

. (2.70)

(2.71)

– закон Ома в комплексной форме записи для всей цепи.

. (2.72)

Рис.39

. (2.73)

После определения комплексной амплитуды осуществляем переход к мгновенному значению.

.

(2.74)

– комплексные действующие значения.

Поиск по сайту: