Явление взаимоиндукции. Взаимная индуктивность

Рис.63

Поток самоиндукции первой катушки можно разделить на два: поток рассеяния , сцепляющийся только с первой катушкой и поток взаимоиндукции , сцепляющийся также со второй катушкой.

. (3.1)

Аналогично для второй катушки:

. (3.2)

Полное потокосцепление первой катушки:

. (3.3)

. (3.4)

. (3.5)

. (3.6)

На рисунке потоки и направлены одинаково, говорят «согласно». Поэтому в скобках перед стоит (+).

Если изменить направление тока в катушке 2, то потоки будут направленны встречно и будет знак(-).

В общем случае:

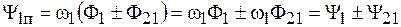, (3.7)

(+) – согласное, (-) – встречное.

– потокосцепление самоиндукции,

– потокосцепление взаимоиндукции.

Величина пропорциональна :

, (3.8)

, (3.9)

– индуктивность первой катушки,

– взаимная индуктивность.

Аналогично для второй катушки:

, (3.10)

. (3.11)

Полная ЭДС, индуктированная в первом контуре:

, (3.12)

=const, , , =const.

Явление наведения ЭДС в каком-либо контуре при изменение тока в другом контуре, называется взаимоиндукцией.

Наведённую ЭДС называют ЭДС взаимоиндукции и обозначают:

– ЭДС взаимоиндукции в первой катушке. (3.13)

. (3.14)

В этих формулах:

, .

.

– напряжение взаимоиндукции (направление, уравновешивающее ЭДС взаимоиндукции).

. (3.15)

В комплексной форме записи:

. (3.16)

. (3.17)

Степени индуктивной связи катушки определяются с помощью коэффициентов связи:

. (3.18)

Поскольку у реальных катушек всегда существуют потоки рассеяния, то .

После простых математических преобразований можно получить

. (3.19)

Поиск по сайту: