 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ИНФОРМАЦИИ
Кодирование информации в ЭВМ - одна из задач теории кодирования. Теория кодирования - один из разделов теоретической информатики. Одна из задач - разработка принципов наиболее экономичного кодирования. Эта задача касается передачи, обработки, хранения информации. Частное ее решение – представление информации в компьютере.
Определение. Алфавит, в котором источник информации представляет сообщение, называется первичным.
Определение. Алфавит, в котором представлено сообщение после обработки в кодирующем устройстве, называется вторичным.
Кодирование – перевод сообщения из первичного алфавита во вторичный. Декодирование – операция обратная кодированию.
Операции кодирования и декодирования называются обратимыми, если их последовательное применение обеспечит возврат к исходной информации без каких-либо ее потерь.
Утверждение. Пусть первичный алфавит А сост. из N знаков со средней информацией на знак IА , вторичный В – из М знаков со средней информацией на знак I В. Пусть сообщение в первичном алфавите содержит n знаков, а закодированное – m знаков. Если исходное сообщение содержит IS (A) информации, а закодированное If (B), то условие обратимости кодирования (то есть неисчезновения информации при кодировании) очевидно может быть записано так:
IS (A) ≤ If (B)
или
n* I (A) ≤ m* I (B)
То есть операция обратимого кодирования может увеличить количество информации в сообщении, но не может уменьшить ее.
Определение. Среднее число знаков вторичного алфавита, который используется для кодирования одного знака первичного назовем длиной кода.
К (А, В)=m/n
Тогда
К (А, В)≥ I (A) / I (B)
Минимально возможная длина кода:
Кmin (А, В)= I (A) / I (B) .
Теорема (первая теорема Шеннона). При отсутствии помех всегда возможен такой вариант кодирования сообщения, при котором средняя длина кода будет сколь угодно близкой к отношению средних информаций на знак первичного и вторичного алфавитов.
При кодировании длина кода может быть одинаковой для всех знаков первичного алфавита (код равномерный) или различной (неравномерный код). Коды могут строиться для отдельного знака первичного алфавита (алфавитное кодирование) или для их комбинаций (кодирование блоков, слов).
Пример. Представление символьной информации в компьютере.
Определим, какой должна быть длина кода. Компьютерный алфавит С включает 52 буквы латинского алфавита, 66 букв русского (прописные и строчные), цифры 0…9, 20 символов для обозначения знаков математических операций, препинания и т.д. В сумме получается 148 символов.
Вычислим длину кода: К (С, 2) ≥ log2 148 ≥ 7,21, но длина кода – целое число, следовательно, К (С,2) =8. Именно такой способ кодирования принят в компьютерных системах. Называют 8 бит =1 байт, а кодирование байтовым. Один байт соответствует количеству информации в одном знаке алфавита при их равновероятном распределении.
Символы в компьютере хранятся в виде числового кода, причем каждому символу ставиться в соответствии своя уникальная комбинация двоичных разрядов. В этом случае текст будет представлен как длинный ряд битов, в котором следующее друг за другом комбинации битов отражают последовательность символов в исходном тексте. Присвоение символу конкретного двоичного кода это вопрос соглашения, которое фиксируется в кодовой таблице – их существует несколько.
Таблица, в которой устанавливается однозначное соответствие между символами и их порядковыми номерами, называется таблицей кодировки.
С распространением ПК типа IBM PC международным стандартом стала таблица кодировки под названием American Standard Cod for Information Interchange – ASCII. Системы кодирования текстовых данных были разработаны и в других странах. Так, например, в СССР в этой области действовала система кодирования КОИ-7 и КОИ-8. Система, основанная на 16-разрядном кодировании символов, получила название универсальной Unicode. Шестнадцать разрядов позволяют обеспечить уникальные коды для 65536 различных символов – этого поля достаточно для размещения в одной таблице символов большинства языков планеты.
V. СИСТЕМЫ СЧИСЛЕНИЯ
Системой счисления называется представление чисел с помощью комбинации знаков. Количество этих знаков образуют основание системы счисления.
Система счисления называется позиционной, если значение знака изменяется в зависимости от его места в числе.
Система счисления называется не позиционной, если значение знака не зависит от его места в числе.
Например, в десятичной системе счисления в числе 118, значение знака «единица» разное. В римской системе счисления это число представляется в виде: CXVIII, здесь знак «единица» имеет одно и то же значение, поэтому десятичная система счисления является позиционной, а римская система счисления не является позиционной. В дальнейшем будем рассматривать только позиционные системы счисления.
В десятичной системе счисления для изображения числа используются следующие десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Числа большей величины, как, например, триста семьдесят два, представляются в виде:
300 + 70 + 2 = 3 × 10  + 7 × 10 + 2
+ 7 × 10 + 2
и в десятичной системе записываются 372. Существенно в данном случае то, что смысл каждой из цифр — 3, 7, 2 — зависит от ее положения — от того, стоит ли она на месте единиц, десятков или сотен. Общее правило такого изображения дается схемой, которая иллюстрируется примером:
z = a × 10 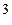 + b × 10
+ b × 10  + c × 10 + d,
+ c × 10 + d,
где, a, b, c, d —– целые числа в пределах от нуля до девяти. Число z в этом случае сокращенно обозначается символом
a b c d.
Заметим, между прочим, что коэффициенты d, c, b, а являются не чем иным, как остатками при последовательном делении числа z на 10.
 Так, например,
Так, например,



 372 10
372 10
2 37 10



 7 3 10
7 3 10
3 0.
С помощью написанного выше выражения для числа z можно изображать только те числа, которые меньше десяти тысяч, так как числа, большие, чем десять тысяч, требуют пяти или большего числа цифр. Если z есть число, заключенное между десятью тысячами и ста тысячами, то можно представлять его в виде:
z = a × 10  + b × 10
+ b × 10 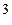 + c × 10
+ c × 10  + d × 10 + e
+ d × 10 + e
и тогда записать символически abcde. Подобное же утверждение справедливо относительно чисел, заключенных между ста тысячами и одним миллионом и т. д. Чрезвычайно важно располагать способом, позволяющим получить результат посредством одной единственной формулы. Этой цели можно добиться, если обозначить различные коэффициенты e, d, c … одной и той же буквой a с различными значками (индексами) а  , а
, а  , а
, а 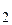 ,…, а степени числа 10 выразим как 10
,…, а степени числа 10 выразим как 10  , понимая под n произвольное натуральное число. В таком случае любое целое число z в десятичной системе может быть представлено в виде:
, понимая под n произвольное натуральное число. В таком случае любое целое число z в десятичной системе может быть представлено в виде:
z = a  × 10
× 10  + a
+ a 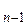 × 10
× 10  + … + a
+ … + a  × 10 + a
× 10 + a 
и записано посредством символа
a  a
a 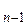 a
a  … a
… a 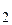 a
a  .
.
Как и в частном, рассмотренном выше, мы обнаруживаем, что a  , a
, a  , a
, a 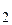 ,…, a
,…, a  являются остатками при последовательном делении z на 10.
являются остатками при последовательном делении z на 10.
В десятичной системе число десять играет особую роль как «основание» системы. Тот, кому приходится встречаться лишь с практическими вычислениями, может не отдавать себе отчет в том, что такое выделение числа десять не является существенным и что роль основания способно было бы играть любое целое число, большее единицы. Например, была бы вполне возможна семеричная (септимальная) система с основанием семь. В такой системе целое число представлялось бы в виде:
b  × 7
× 7  + b
+ b 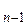 × 7
× 7  + … + b
+ … + b  × 7 + b
× 7 + b  ,
,
где b – коэффициенты, обозначающие числа в пределах от нуля до шести. Тогда такое целое число записывалось бы посредством символа b  b
b 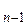 … b
… b  b
b  .
.
Так, число «сто девять» в семеричной системе обозначалось бы символом 214, потому что
109 = 2 × 7  + 1 × 7 + 4.
+ 1 × 7 + 4.
В качестве упражнения можно вывести общее правило для перехода от основания 10 к любому основанию р: нужно выполнять последовательное деление на р, начиная с данного числа z; остатки и будут «цифрами» при записи числа в системе с основанием р. Например,
 109 7
109 7





 4 15 7
4 15 7
3 2 7

 1 2 0.
1 2 0.
109 (в десятичной системе) = 214 (в семеричной системе).
Поиск по сайту: