 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Изображение целых значений в позиционных системах счисления: десятичная, двоичная и шестнадцатеричная системы
Введем для общности понятие об изображении целых числовых значений в системе счисления с основанием р, где р — целое число, р ≥ 2. Цифрами в системе счисления с основанием р называют р символов, обозначающих все целые значения от 0 до р – 1.
В десятичной системе счисления (р = 10) такими символами являются
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В двоичной системе счисления (р = 2) в качестве цифр употребляются символы 0 и 1.
В шестнадцатеричной или hex -системе счисления в качестве цифр используются символы
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Изображение целого числового значения N в виде строки
c  c
c  … c
… c  (n ≥ 0) (1)
(n ≥ 0) (1)
в р -ичной системе счисления (c  — цифры этой системы счисления) значение N определяют формулой: N = c
— цифры этой системы счисления) значение N определяют формулой: N = c  p
p  + c
+ c  p
p 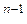 + … + c
+ … + c  p
p  . (2)
. (2)
Из формулы (2) следует, в частности, что p  в р -ичной системе счисления изображается последовательностью k +1 символов, из которых первый — 1, а остальные k — нули, например:
в р -ичной системе счисления изображается последовательностью k +1 символов, из которых первый — 1, а остальные k — нули, например:
10  = (1000)
= (1000)  ; 16 = (10)
; 16 = (10)  ; 16
; 16  = (100)
= (100)  ;
;
2 = (10)  ; 2
; 2  = (10000)
= (10000)  и т. п.
и т. п.
Индексом справа внизу обозначено основание системы счисления, в которой представлено число в скобках.
С помощью формулы (2), зная изображение (1) в р -ичной системе счисления, можно получить изображение значения N в q -ичной системе счисления. Для этого нужно изобразить c  и р в q -ичной системе счисления и выполнить действия, предписанные формулой (2) по правилам «q -ичной арифметики».
и р в q -ичной системе счисления и выполнить действия, предписанные формулой (2) по правилам «q -ичной арифметики».
Если q = 10, то эти действия — перевод изображения из р -ичной системы счисления в его изображение в десятичной системе — выполняются с помощью привычной нам десятичной арифметики. Рассмотрим примеры.
Пусть р = 2 и задано изображение некоторого значения в двоичной системе счисления:
1111011 (3)
Тогда в соответствии с формулой (2) десятичное изображение этого значения определяется выполнением действий:
1 ∙ 2 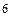 + 1 ∙ 2
+ 1 ∙ 2  + 1 ∙ 2
+ 1 ∙ 2  + 1 ∙ 2
+ 1 ∙ 2  + 0 ∙ 2
+ 0 ∙ 2  + 1 ∙ 2
+ 1 ∙ 2  + 1 ∙ 2
+ 1 ∙ 2  . (4)
. (4)
Вычислив выражение (4), получим десятичное изображение значения, представленного в двоичной системе в виде (3): 123, т. е.:
(1111011) 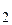 = (123)
= (123)  .
.
Пусть теперь р = 16 и задано изображение некоторого значения в шестнадцатеричной системе счисления AF 01.
Для получения десятичного изображения этого значения подставим в формулу (2) десятичные представления шестнадцати шестнадцатеричных цифр и показателей степеней 10 ∙16  + 15 ∙16
+ 15 ∙16  + 0 ∙ 16
+ 0 ∙ 16 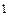 + 1 ∙ 16
+ 1 ∙ 16  = 44801,т. е.:
= 44801,т. е.:
(AF01)  = (44801)
= (44801)  .
.
Для перевода десятичного (р = 10) изображения значения в его изображение в какой-нибудь «чужой» системе счисления (например, q = 16) следовало бы, пользуясь формулой (2), подставлять в нее шестнадцатеричные изображения степеней десяти и проводить умножение и сложение в шестнадцатеричной системе. Однако человеку действовать по правилам шестнадцатеричной системы неудобно. Поэтому для перевода вручную изображений числовых значений из десятичной системы счисления в шестнадцатеричную используется другой прием.
Пусть известно десятичное изображение N. Из формулы (2) следует: значение младшей шестнадцатеричной цифры с  является остатком от деления N на 16, а частное этого деления N
является остатком от деления N на 16, а частное этого деления N  = с
= с  + с
+ с  16
16 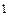 + … с
+ … с  16
16 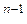 . Таким образом, с
. Таким образом, с  , с
, с  , с
, с  и т. д. будут являться остатками от деления N, N
и т. д. будут являться остатками от деления N, N  , N
, N  , … и т. д. на 16. Деление продолжается до тех пор, пока очередное частное не окажется равным нулю.
, … и т. д. на 16. Деление продолжается до тех пор, пока очередное частное не окажется равным нулю.
Например, получение десятичного значения N = 44801 в шестнадцатеричной системе счисления выполняется так:
44801|16

 остаток: 1|2800| 16
остаток: 1|2800| 16
 остаток: 0 ׀ 175|16
остаток: 0 ׀ 175|16
 остаток: 15 | 10 | 16
остаток: 15 | 10 | 16
 остаток: 10 | 0
остаток: 10 | 0
Таким образом, значения шестнадцатеричных цифр равны соответственно значениям остатков 1, 0, 15, 10 (в десятичном представлении). Заменяя эти значения их шестнадцатеричным изображением, получим:
(44801)  = (AF 01)
= (AF 01)  .
.
Можно доказать следующее простое правило перехода от двоичного изображения числового значения к его шестнадцатеричному изображению и обратно. Для этого достаточно (дополнив, если надо, двоичное изображение незначащими нулями слева) заменить каждую четверку двоичных цифр (тетраду) шестнадцатеричной цифрой, изображающей значение этого четырехразрядного двоичного числа (табл. 1).
Таблица 1
Поиск по сайту: