 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Изображение дробных чисел в двоичной и шестнадцатеричной системах счисления
Изображением дроби в какой-либо системе счисления называется последовательность вида:
0. а  а
а 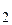 … а
… а  . (5)
. (5)
Ноль и точка выполняют роль признака правильной дроби; а — цифры в соответствующей системе счисления. Приписывание любого числа незначащих нулей слева от 0 или справа от а  не меняет изображаемого значения. Значение дроби (5) есть значение выражения: Q = a
не меняет изображаемого значения. Значение дроби (5) есть значение выражения: Q = a  p
p  + a
+ a  p
p  + … + a
+ … + a  p
p  , (6)
, (6)
где р – целое значение – основание системы счисления.
Для перевода двоичного или шестнадцатеричного изображения дроби в десятичное нужно подставить в выражение (6) десятичное изображение а  и р и выполнить действия по правилам десятичной арифметики. Например:
и р и выполнить действия по правилам десятичной арифметики. Например:
(0.1001101)  = 1∙2
= 1∙2  +0∙2
+0∙2  +0∙2
+0∙2  +1∙2
+1∙2  +1∙2
+1∙2  +0∙2
+0∙2  +1∙2
+1∙2  = (0.6015625)
= (0.6015625)  ;
;
(0.9 А)  = 9∙16
= 9∙16  + 10∙16
+ 10∙16  =(0.6015625)
=(0.6015625)  .
.
Чтобы получить двоичное или шестнадцатеричное изображение значения дроби Q, заданной десятичным представлением, умножают Q по правилам десятичной арифметики на 2 (или 16); значение целой части произведения a  изображают цифрой двоичной (шестнадцатеричной) системы. Если дробная часть Q
изображают цифрой двоичной (шестнадцатеричной) системы. Если дробная часть Q  произведения не ноль, то Q
произведения не ноль, то Q  умножают на 2 (16) и тем же путем получают значение цифры a
умножают на 2 (16) и тем же путем получают значение цифры a 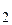 и т. д.
и т. д.
Переведем, например, десятичную дробь 0.6015625 в двоичную и шестнадцатеричную системы счисления:
0.6015625 ∙ 2 = 1.203125, a  = 1;
= 1;
0.203125 ∙ 2 = 0.40625, a  = 0;
= 0;
0.40625 ∙ 2 = 0.8125, a  = 0;
= 0;
0.8125 ∙ 2 = 1.625, a  = 1;
= 1;
0.625 ∙ 2 = 1.25, a  = 1;
= 1;
0.25 ∙ 2 = 0.5, a  = 0;
= 0;
0.5 ∙ 2 = 1.0, a  = 1.
= 1.
Искомое двоичное представление 0.1001101.
0.6015625 ∙ 16 = 9.625, a  = (9)
= (9)  = (9)
= (9)  ;
;
0.625 ∙ 16 = 10.00, a  = (10)
= (10)  = (А)
= (А)  .
.
Шестнадцатеричное представление 0.9А.
Между цифрами двоичных и шестнадцатеричных изображений дробей существует такая же простая связь, как между цифрами двоичных и шестнадцатеричных представлений целых значений, в чем можно убедиться на предыдущем примере.
Поиск по сайту: