Модели выживаемости распределенной информационной системы

Увы, в реальной практике риск-анализа статистическое исследование приходится проводить по неполным данным. Допустим, исследуется выход из строя распределённой информационной системы (РИС) после атаки на одну из её компонент: начало исследования – момент проведённой атаки; исследуемый период времени выбирается в зависимости от конкретного типа атаки и возможных последствий; наблюдаемое событие – состояние работоспособности конкретной компоненты и выход из строя всей системы. Аккумулируя данные наблюдений от времени начала атак до выхода из строя за большим числом аналогичных (схожих) систем их компонентов, можно получить достаточно полную картину процесса протекания негативных последствий в следствии реализации того или иного деструктивного воздействия. Но, чем длиннее временной промежуток исследования, тем более вероятно вмешательство побочных факторов (наблюдаемая система подверглась воздействию других деструктивных воздействий, устарела или её функционирование стало экономически неоправданным и.т.п.) Такое наблюдение нельзя считать абсолютно качественным, так как оно так же связано с разным временем начала отсчёта в каждом наблюдении. Поэтому в реальных задачах бессмысленно стремиться к максимальной полноте, а следует полноценно использовать имеющиеся данные, пусть и неполные. С учётом вышеуказанного рассмотрим анализ выживаемости, где наблюдаемым событием является безвозвратный выход из строя системы (подсистемы, компоненты и т.п.). При этом, цензурированное наблюдение– это наблюдение, по каким-то причинам не закончившееся искомым событием: то ли вследствие окончания наблюдаемого периода, то ли по внешним причинам (при рассмотрении РИС различного уровня получение цензурированных данных о состоянии конкретной компоненты возможно в следствии целого набора причин, например атака на информационный канал связи и управления, атака на систему оценки работоспособности и т.п.). Информацией, содержащейся в полном наблюдении, является длина временного промежутка от начала отсчёта до осуществления события. В цензурируемом наблюдении содержится информация о том, что за время от начала до окончания наблюдения событие не произошло.

В анализе выживаемости РИС постараемся использовать всю имеющуюся информацию, содержащуюся как в полных, так и в цензурированных данных.

Известно несколько механизмов, генерирования цензурированных данных. При цензурировании первого типа выборка из n объектов наблюдается в течении фиксированного времени τ. Число объектов, испытывающих событие, или число «смертей», случайно, но общая продолжительность исследования фиксирована. Тот факт, что продолжительность фиксирована, может быть важным практическим преимуществом при разработке последующего дополнительного исследования. При таком цензурировании, называемом фиксированным цензурированием, каждый объект имеет максимально возможный период наблюдения 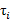, i= 1,…,n, который может варьироваться от одного объекта к другому, однако фиксирован заранее. Вероятность того, что объект i будет жив в конце своего периода наблюдения, равна S(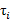), а общее число смертей вновь является случайным. При цензурировании второго типа выборка из n объектов наблюдается так долго, сколько необходимо, чтобы d объектов испытали событие. В этой схеме число смертей d, которое определяет точность исследования, фиксировано заранее и его можно использовать в качестве параметра. К сожалению, в этом случае общая продолжительность исследования случайна и не может быть точно известна заранее. При более общей схеме, называемой случайным цензурированием, каждый объект имеет потенциальный момент цензурирования и потенциальную продолжительность жизни , которые предполагаются независимыми случайными величинами. Наблюдается =min , то есть минимум из времени цензурирования и времени жизни, и переменная-индикатор, часто обозначаемая , которая указывает, закончено наблюдение в результате смерти или цензурирования. Обе схемы ведут к той же самой функции правдоподобия. Цензурирование наблюдения не должно давать какой-либо информации относительно перспектив выживания этого конкретного объекта за пределами момента цензурирования. Все, что известно о наблюдении, цензурированном в момент времени t, – это то, что время жизни для него превышает t.

Допустим имеется РИС, состоящая из n компонентов наблюдения со временем их жизни, характеризуемым функцией выживания с соответствующей плотностью и риском Risk(t). Предположим также, что компонент i наблюдается в течение времени t_i. Если компонент i вышел из строя в момент , то его вклад в функцию правдоподобия – значение плотности в этот момент времени, можно записать как произведение функций выживания и риска:

.

Если компонент РИС все еще продолжает выполнять функции, несмотря на дестабилизирующее воздействие со стороны злоумышленника, в момент времени , то все, что известно при неинформативном цензурировании – это то, что время его «жизни» превышает . Вероятность этого события равна , и отражает вклад цензурированного наблюдения в функцию правдоподобия. Оба варианта вкладов содержат функцию выживания S(), поскольку в обоих случаях компонент продолжал выполнять функции до момента времени . Прекращение функционирования объекта («смерть» компоненты) как бы «домножает» этот вклад на риск , а цензурирование – нет. Можно записать оба типа вкладов в виде единого выражения. Для этого пусть является индикатором смерти и равняется единице, если компонент i умер, и нулю в противном случае.

Если компонент РИС все еще «жив» в момент времени что известно при неинформативном цензурировании – это то, что время его «жизни» превышает 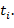Вероятность этого события равна

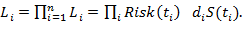
Логарифмируя и используя выражение, связывающее функцию выживания и функцию кумулятивного риска , получаем логарифмическую функцию правдоподобия для цензурированных данных о выживаемости:

Вышеуказанные выражения позволяют оценить неизвестные параметры, основанные на известных результатах, то есть вероятность возникновения определенного события с помощью логарифмической функции правдоподобия.

Допустим, начало наблюдения определяется неким фактом, скажем, атакой на РИС. Контролируемое событие – прекращение выполнения возложенных функций на наблюдаемый компонент РИС вследствие успешной атаки злоумышленника, («смерть» компоненты) – является случайным событием. Время от начала наблюдения до «смерти» – случайная величина Т, тогда значения этой случайной величины – t. Эта случайная величина неотрицательная и непрерывная, имеет свой закон распределения, априори неизвестный. Функция распределения случайной величины равна

где F(t) – вероятность не «дожить» до момента времени t от начала отсчета. При t<0 обязательно F(t) = 0, а при положительном аргументе F(t) – функция возрастающая (точнее, неубывающая), с ростом t стремящаяся к 1.

Функция распределения F(t) служит вероятностной характеристикой рассматриваемого процесса. По функции распределения F(t) можно найти соответствующую плотность распределения вероятностей f(t) как производную f(t) = (t).

Обычно исследуемый процесс времени «жизни» целесообразнее связывать не с функцией распределения F(t), а с дополняющей до единицы функцией (функция выживания)

(4)

так как

). (5)

Согласно свойству вероятностей противоположных событий, то S(t) – вероятность штатного (с сохранением основных функций) функционирования компоненты РИС по истечении момента времени t с начала активного дестабилизирующего воздействия (прожить время, большее T),поэтому функцию S(t) заданную соотношениями (4) и (5), называют функцией «выживания» (выживаемостью). Кривая функции «выживания» S(t) легко может быть построена исходя из графика функции распределения F(t) и соотношения (5). Стоит также отметить, что для функции S(t) значения функции при t<0 не имеют смысла.

Можно вычислить функцию выживания через интегрирование:

(6)

определяя вероятность быть «живым» в момент времени t, или в более широком смысле, вероятность того, что исследуемое событие не наступило к моменту времени t.

График функции y=S(t) называют кривой выживаемости. Значение, при котором S(τ_0.5)=0,5 называется медианой выживаемости, которая совпадает с медианой распределения случайной величины Т. Медиана выживаемости является одной из важнейших характеристик выживаемости: она указывает середину теоретического времени жизни отдельного компонента системы после начала отсчета (в качестве начала отсчета может быть рассмотрена активная фаза атаки на компоненты РИС). Аналогично квантилям распределения порядка р, где 0<p<1, обозначаемым t_p, используют квантили выживаемости. Обозначим квантиль выживаемости порядка р посредством τ_р, где S(τ_р)=p. Тогда для квантилей выживаемости и соответствующих квантилей распределения справедливо соотношение

τ_р=t_1-p, (7)

т.е. квантиль выживаемости порядка р является квантилью распеделения порядка 1-р. Соотношение (7) можно легко получит из (6):

,

следовательно

где, значение распределения случайной величины Т порядка (1-р).

Кривая выживаемости y=S(t), построенная по распределению случайной величины Т является теоретической кривой, характеризующей процесс продолжительности «жизни». Соответствующие характеристики выживаемости согласованы с вероятностным распределением, поэтому, значения квантильной широты, определяемой как расстояние между двумя точками (квантилями кривых), в обоих случаях совпадают:

Возможно охарактеризовать величины Т с помощью функции риска- мгновенной интенсивности осуществления события

(8)

В числители этого выражения (8) находится условная вероятность того, что событие произойдет в интервале времени (, + ), если оно не произошло ранее, а знаменатель – ширина интервала. Разделив одно на другое, получаем интенсивность осуществление события в единицу времени. Устремляя ширину интервала к нулю и переходя к пределу, получаем мгновенную интенсивность осуществления события.

Условную вероятность в числителе можно записать в виде отношения совместной вероятности того, что Т принадлежит интервалу (, + ) и (что совпадает с вероятностью того, что Т принадлежит указанному интервалу), к вероятности условия . Первая из них равна для малого а последняя это , по определению. Деление на и предельный переход дают следующий результат:

(9)

который и является определением функции риска. Интенсивность осуществления события в момент времени равна плотности событий в момент , деленной на вероятность дожить до этого момента, не испытав событие ранее.

Учитывая, что - это производная уравнение (9) можно записать в виде

Если теперь проинтегрировать обе части от 0 до и ввести граничное условие (поскольку событие не может произойти к моменту времени 0), можно преобразовать приведенное выражение и получить формулу для вероятности работоспособности компонента РИС (вероятности «дожить») до момента времени t как функции от рисков во все моменты времени до t:

(10)

Интеграл в фигурных скобках в уравнении (7) называют кумулятивным риском

который можно рассматривать как сумму всех рисков при переходе от момента времени 0 к t, т.е. интегральным риском.

Фактически функции выживания и риска дают альтернативные, но эквивалентные описания распределения величины Т. Имея функцию выживания, можно ее продифференцировать и получить функцию плотности, а затем найти функцию риска. Зная функцию риска, можно ее проинтегрировать и получить кумулятивный риск, а затем от нее экспоненту и найти функции выживания, используя уравнение (10).

Для задач с дискретным временем всегда определены вероятности

В дискретном случае риск можно определить по формуле:

где и

Риск может быть любой неотрицательной функцией, в случае дискретного времени не превосходящей 1, выживаемость 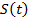- неотрицательной, начинающейся со значением 1 и монотонно невозрастающей, а условие = 0 равносильно расходимости интеграла при непрерывном времени или ряда при дискретном.

Для системы из n элементов с разными распределениями времени жизни { } и соответственно, функциями выживаемости { } можно определить усредненную функцию выживаемости, 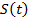равную математическому ожиданию доли объектов, выживших к моменту t:

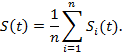
Плотность и функция распределения получившегося «усредненного» объекта также равны средним арифметическим соответствующих функций элементов.

Производительность (нормированная) компоненты РИС может быть также описана с помощью выражения

где и - постоянные времени «восхода» и «заката» компоненты системы. Раскрывая последнее выражение, имеем

Следует заметить, что текущее время t и параметры , пронормированы по средней продолжительности жизни компоненты 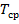, т.е.

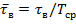, и

При этом, ценность компоненты в момент времени измеряется через ее эффективность. В случае досрочной «гибели» компоненты эта ценность составит величину ущерба как сумму упущенной выгоды

.

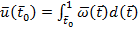Учитывая, что смертность наиболее высока в период «заката», выражение эффективности (11) можно упростить с помощью следующего приближения

Отсюда ущерб равен

Последнее выражение может послужить основой для оценки рисков выживаемости компонент распределенной системы в следующем виде

Risk 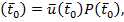(12)

где ,

– шаг дискретизации плотности вероятности

Как видно, последнее выражение (12) существенно отличается от вышеприведенных риск-оценок РИС. Однако такой подход (12) следует считать наиболее адекватным, ибо он опирается на величину ущерба, как этого и требует истинная оценка риска.

Адекватность оценки может быть еще повышена, если для измерения ущерба используется все выражение (11), тогда

Соответствующее аналитическое выражение риска может быть получено отсюда по аналогии с вышеуказанным.

Общий риск РИС может быть найден как сумма рисков ее компонентов при условии существенной их независимости друг от друга. Такой подход корректен при условии, что атаки носят асинхронный характер, т.е. их вероятность подлежит суммированию.

Поиск по сайту: