 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Концепция временного риск-анализа распределенных систем: аналитические выражения риска
Основы оценки рисков и защищенности компьютерно атакуемых информационных систем и технологий
Учебное пособие
для выполнения индивидуальных заданий практических занятий и производственных практик, курсового и дипломного проектирования
Утверждено Редакционно-издательским советом
университета в качестве учебного пособия
Воронеж 2013
Концепция временного риск-анализа распределенных систем: аналитические выражения риска
Мы оставляем за «кадром» методы нечеткого вывода и нечеткие множества, которые успешно работают при «корректных» экспертных оценках и дают в этом случае удовлетворительные риск-оценки. Примером тому может служить материал монографии Щербакова В.Б. [1].
В тех случаях, когда система располагает емкой статистикой о своем поведении и/или поведении подобных систем в условиях воздействия на них дестабилизирующих факторов (атак), уместно пользоваться иными подходами. Один из них предлагался в монографиях Остапенко Г.А. и Белоножкина В.И. [2-4] получивших премию правительства Воронежской области (в области науки).
Ниже предлагается обобщение и развитие этой методологии применительно к риск-анализу распределенных систем и процессов различного назначения.
1) Для нахождения риска появления негативного события в момент времени  c точностью
c точностью  уместно воспользоваться следующей иллюстрацией (рис. 1).
уместно воспользоваться следующей иллюстрацией (рис. 1).
| t0 |
| f(t0) |
| Dt |
| t |
| f(t) |
Рис. 1. Пример дискретизации плотности вероятности
где: 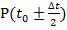 – есть искомая вероятность и площадь выделенного сегмента;
– есть искомая вероятность и площадь выделенного сегмента;
 - плотность вероятности;
- плотность вероятности;
 – интервал дискретизации;
– интервал дискретизации;
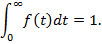
Отсюда вероятность того, что событие произойдет в интервале 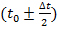 приближенно можно (для малых
приближенно можно (для малых  ) определить так
) определить так
 , где
, где 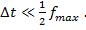
Тогда риск равен:
 , где u-ущерб (1)
, где u-ущерб (1)
2) Для нахождения вероятности появления негативного события в интервале (0,  ) следует воспользоваться нижеприведенным рисунком (рис. 2),
) следует воспользоваться нижеприведенным рисунком (рис. 2),
| f(t) |

Рис. 2. Нахождение накопленной вероятности
где  – искомая вероятность площадь выделенного сегмента.
– искомая вероятность площадь выделенного сегмента.
Вероятность того, что событие произойдет в интервале  ) равна
) равна
 .
.
Ущерб, видимо, придется усреднять и тогда:
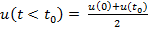 .
.
Отсюда риск усреднено равен будет
 .
.
Точнее риск можно найти через интегральное усреднение в интервале (0,  ). Тогда
). Тогда
 . (2)
. (2)
3) Поиск вероятности события в интервале ( ,
, 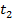 ) иллюстрирует следующий рисунок (рис. 3)
) иллюстрирует следующий рисунок (рис. 3)
| f(t) |
| t2 |
| t1 |
| f(t1) |
| f(t2) |
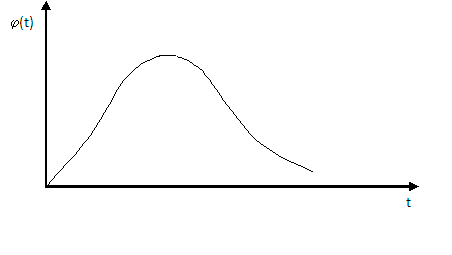
Рис. 3. Нахождение интервальной вероятности
 – искомая вероятность и площадь выделенного сегмента.
– искомая вероятность и площадь выделенного сегмента.
Риск того, что событие произойдет в период времени  будет равен
будет равен
 . (3)
. (3)
Или приближенно

Все три варианта, рассмотренных на рис. 1-3 имеют практическое значение, которое будет раскрыто далее.
Для анализа жизнестойкости уместно производить нормирование шкалы времени t по средней продолжительности жизни исследуемого объекта 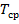 . Тогда нормированное время будет равно
. Тогда нормированное время будет равно

и все дальнейшие выкладки следует уже производить с этой переменной, а кривая плотности вероятности примет следующий вид (рис. 4)

|

|
Рис. 4. Плотность вероятности при нормировании временем
Далее следует определить функцию ущерба. В зависимости от времени в общем виде она для фатального исхода (т.е. гибели объекта или утраты им работоспособности безвозвратно) может быть нормировано, выражена в следующем аналитическом виде.
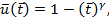
где ущерб пронормирован по своему максимально возможному значению (максимальной ценности объекта в период жизни 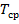 ) и
) и 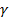 является показателем нелинейности данной зависимости (
является показателем нелинейности данной зависимости ( , при
, при  она линейная).
она линейная).
Отсюда усредненный ущерб составит:
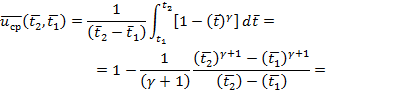
 ,
,
где: при  имеем
имеем 
 , а при
, а при  получаем
получаем
 .
.
Кривая ущерба в этом случае выглядит так (рис. 5),

|
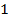
|
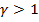
|

|
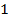
|

|
Рис. 5. Кривая зависимости ущерба от времени
что согласуется с физическим смыслом (ценность утраченного объекта убывает при приближению к среднему времени его жизни).
В итоге усреднено риск гибели объекта в интервале времени  составит:
составит:

Если нам необходимо найти риск того, что система «не доживет» до времени  , то
, то
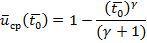
и усреднено имеем

Когда требуется оценить риск того, что объект «скончается» в окрестности  времени
времени  , уместно воспользоваться приближенным выражением
, уместно воспользоваться приближенным выражением

Чем меньше  , тем выше точность приближения.
, тем выше точность приближения.
Иначе обстоит дело при временной утрате работоспособности объекта. В этом случае учитывается период  и производительность
и производительность  объектом пользы во времени. Тогда ущерб можно оценить следующим образом
объектом пользы во времени. Тогда ущерб можно оценить следующим образом

где  – средняя производительность за время жизни
– средняя производительность за время жизни 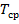 .
.
Один из вариантов поиска этой функции представлен на следующем рис. 6,

|

|

|

|

|
Рис. 6. Зависимость производительности от времени жизни системы
где 1<b и 
При нормировании по  имеем:
имеем:

Перейдем теперь к оценке ущерба. Отсюда:
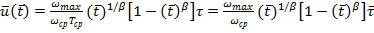 , где
, где 
Причем:

Тогда риск равен:

Данная концепция учитывает только нормированную упущенную выгоду из-за простоя (отказа) при  . В общем случае в последнем выражении следует добавить затраты на устранение отказа
. В общем случае в последнем выражении следует добавить затраты на устранение отказа

которые зависят от  и
и  .
.
Уместно заметить, что функция  носит колоколобразный характер, так как эффективность объекта в период его запуска в эксплуатацию (старт) и в период старения (финиш) очевидно ниже штатного уровня
носит колоколобразный характер, так как эффективность объекта в период его запуска в эксплуатацию (старт) и в период старения (финиш) очевидно ниже штатного уровня  (рис. 7). Интересно заметить, что
(рис. 7). Интересно заметить, что  , штатный режим достигает 80% от
, штатный режим достигает 80% от 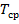 .
.
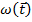

|

|
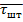
|
Рис. 7. Зависимость эффективности с учетом штатного режима
Для длительных простоев необходимо учитывать зависимость  от времени, однако в штатном режиме ошибки будут здесь незначительны и при
от времени, однако в штатном режиме ошибки будут здесь незначительны и при  ущерб примерно будет равен
ущерб примерно будет равен
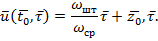
Здесь затраты на восстановление будут почти пропорциональны его времени. Интересно было бы аналитически выразить вышеприведенную кривую.
Что же касается риска, то в момент времени  для интервала простоя он приближенно может быть оценен следующим образом
для интервала простоя он приближенно может быть оценен следующим образом
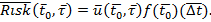
Теоретический и практический интерес представляют результаты монографии Радько Н.М. [5], где на основе сетей Маркова-Петри предлогается находить вероятность осуществления НСД в течении времени t к компоненту системы с помощью следующего выражения
 ,
,
где 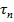 – интегральная длительность прохождения всех необходимых переходов для проникновения в систему вредоноса. Если считать
– интегральная длительность прохождения всех необходимых переходов для проникновения в систему вредоноса. Если считать 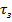 временем активного действия (заражения и т.п.) вредоноса в системе, то по весьма распространенной SIS-модели ущерб (количество испорченных файлов) составит в нормированном виде
временем активного действия (заражения и т.п.) вредоноса в системе, то по весьма распространенной SIS-модели ущерб (количество испорченных файлов) составит в нормированном виде
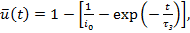
где  – стартовое во время
– стартовое во время  количество зараженных файлов. Полагая
количество зараженных файлов. Полагая  и обозначая
и обозначая  , имеем риск, равный
, имеем риск, равный

Возможны и другие вариации аналитической оценки ущерба по стадиям реализации атаки.
Поскольку распределенные системы рассредоточивают ресурсы и функции в информационном пространстве своих компонентов, то особый интерес представляет риск-анализ по порогам безопасности, которые имеют место быть для каждого ресурсного блока и функции. К примеру, «перебор» в трафике запросов порождает «отключение» функции доступности и т.д. и т.п. Соответствующую типологию операций можно осуществить с помощью другой монографии Остапенко Г.А. [4].
Пусть на интервале  задан единственный (на практике их может быть несколько) порог
задан единственный (на практике их может быть несколько) порог  , превышение которого повлечет утрату заданной функции или ресурса.
, превышение которого повлечет утрату заданной функции или ресурса.  изображен на нижеприведенном рисунке 8, где
изображен на нижеприведенном рисунке 8, где 


|

|
Рис. 8. Временная реализация переменной состояния
При этом, пусть известен закон распределения экстремумов (в данном случае максимумов) переменной состояния  и его описывает плотность вероятности
и его описывает плотность вероятности  ,
,

|

|
Рис. 9. Распределение экстремумов переменной состояния
зависимость которой от величины экстремума (нормированного)  представлена на данном рисунке 9. Что же касается ущерба, то он может представлен рисунком 10,
представлена на данном рисунке 9. Что же касается ущерба, то он может представлен рисунком 10,

|
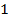
|

|

|
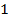
|

|
Рис. 10. Зависимость ущерба от величины экстремума
где 
Отсюда риск в окрестности  может быть выражен как
может быть выражен как

Интересно, что дискретизация значений переменной  с учетом ее нормирования может быть сведена к равенству
с учетом ее нормирования может быть сведена к равенству
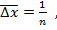 где n- количество дискрет.
где n- количество дискрет.
При этом имеем,
 или
или 
Вышеизложенное относится к так называемым «фатальным» атакам, когда отказ функции или ресурса по порогу безопасности длится больше, чем среднее время жизни. В отличии от них временные отказы предусматривают двойное пересечение порога (туда и обратно) в интервале  . Здесь следует воспользоваться методикой, изложенной выше в отношении производительности анализируемой системы (временная неработоспособность без необратимых явлений).
. Здесь следует воспользоваться методикой, изложенной выше в отношении производительности анализируемой системы (временная неработоспособность без необратимых явлений).
С учетом вышеизложенного следует исследовать аналитические выражения риска, найдя усредненные, пиковые и др. значения конкретно для соответствующего вида распределения  .
.
Применительно к многокомпонентным и особенно распределенным системам вышеприведенные выражения практически могут быть применены следующим образом. При этом, следует исходить из общесистемных соображений, которые кратко можно сформулировать так:
- в штатном режиме функционирования отказы атакуемых компонентов распределенной пространственно и функционально системы слабо коррелированны между собой и их можно рассматривать как взаимоисключающие (чередующиеся) события, вероятности которых складываются;
- при массированной (одновременно на множество компонентов) атаке системы мы имеем дело с совмещенными событиями отказа, вероятности которых перемножаются.
Если ущербы компонентов определены на одной оси (шкале), то аналогичные операции можно осуществить и с рисками отдельных компонент. Для этих двух случаев возможно рассмотрение вариантов, когда компоненты однотипны, т.е. имеют один и тот же закон распределения  Однако следует учитывать, что ценность компонент даже в этом случае может быть различной. Получение таких аналитических выражений представляет теоретический и практический интерес в контексте рассмотренных вариантов нахождения вероятности (1)-(3) и заданного закона распределения
Однако следует учитывать, что ценность компонент даже в этом случае может быть различной. Получение таких аналитических выражений представляет теоретический и практический интерес в контексте рассмотренных вариантов нахождения вероятности (1)-(3) и заданного закона распределения 
Следует заметить, что эта задача нашла достаточно широкое распространение в теории элементарных значений и финансовой эконометрике в части прогнозирования чрезвычайных ситуаций и как инструментарий оценки операционного риска.
Поиск по сайту: