 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Методика расчета линейных цепей при периодических
несинусоидальных токах
Возможность разложения периодических несинусоидальных функций в ряд Фурье позволяет свести расчет линейной цепи при воздействии на нее несинусоидальных ЭДС (или токов) источников к расчету цепей с постоянными и синусоидальными токами в отдельности для каждой гармоники. Мгновенные значения искомых токов и напряжений определяются на основе принципа наложения путем суммирования найденных при расчете гармонических составляющих напряжений и токов. В соответствии с вышесказанным цепь на рис. 5 при воздействии на нее ЭДС
(при расчете спектр рассматриваемых гармоник ограничивается) в расчетном плане представляется суммой цепей на рис. 6.
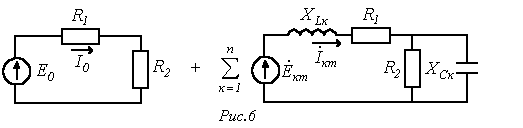
Здесь 
.
Тогда, например, для тока в ветви с источником ЭДС, имеем
,
где каждая к-я гармоника тока рассчитывается символическим методом по своей к-й расчетной схеме. При этом (поверхностный эффект не учитывается) для всех гармоник параметры 
и С постоянны.
;
.
Необходимо помнить, что ввиду различия частот суммировать комплексы различных гармоник недопустимо.
Таким образом, методика расчета линейных цепей при несинусоидальных токах сводится к следующему:
- ЭДС и токи источников раскладываются в ряды Фурье.
- Осуществляется расчет цепи в отдельности для каждой гармонической.
- Искомые величины определяются как алгебраические суммы соответствующих гармонических.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Контрольные вопросы
- Что является причиной появления несинусоидальных токов и напряжений в электрических цепях?
- Какие величины и коэффициенты характеризуют периодические несинусоидальные переменные?
- Какие гармонические отсутствуют в спектрах кривых, симметричных относительно: 1) оси абсцисс; 2) оси ординат; 3) начала системы координат?
- Достаточно ли для определения величины полной мощности в цепи несинусоидального тока наличие информации об активной и реактивной мощностях?
- Для каких цепей справедлива методика расчета цепей несинусоидального тока, основанная на разложении ЭДС и токов источников в ряды Фурье?
- Не прибегая к разложению в ряд Фурье, определить коэффициенты амплитуды и формы кривой на рис. 4.
Ответ: 
.
- Определить действующее значение напряжения на зажимах ветви с последовательным соединением резистора с
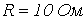и катушки индуктивности с 
, если ток в ней 
. Рассчитать активную мощность в ветви.
Ответ: U=218 В; Р=1260 Вт.
- Определить действующее значение тока в ветви с источником ЭДС в схеме на рис. 5, если
; 
.
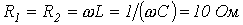Ответ: I=5,5 A.
Для к-й гармоники тока можно записать
,
где 
- действующее значение к-й гармоники ЭДС.
Таким образом, при изменении С величина к-й гармоники тока будет изменяться от нуля при С=0 до 
при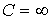 
, достигая максимума 
при резонансе (см. рис. 1,б), определяемом величиной емкости
.
Следует отметить, что, несмотря на то, что обычно с ростом порядка гармонической ЭДС ее амплитуда уменьшается, в режиме резонанса для к-й гармонической ее значение 
может превышать величину первой гармоники тока.
Резонансные явления используются для выделения гармоник одних частот и подавления других. Пусть, например, в цепи на рис. 2 необходимо усилить q-ю гармонику тока на нагрузке и подавить р-ю.
Для подавления р-й гармоники в режим резонанса токов настраивается контур 
:
.
Для выделения q-й гармоники вся цепь для нее настраивается в режим резонанса напряжений:
,
откуда при известных 
и 
.
Отметим, что рассмотренные явления лежат в основе работы L-C -фильтров.
Особенности протекания несинусоидальных токов через пассивные элементы цепи
1. Резистор.
При 
ток через резистор (см. рис. 3)
,
где 
.
Таким образом, на резистивном элементе несинусоидальные напряжение и ток совпадают по форме и подобны друг другу. Это позволяет на практике осциллографировать форму тока с помощью регистрации напряжения на шунте.
2. Конденсатор.
Пусть напряжение на конденсаторе (рис. 4) описывается гармоническим рядом 
.
.
.
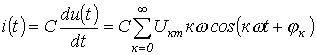, т.е. конденсатор искажает форму кривой тока по сравнению с напряжением, являясь сглаживающим элементом для последнего.
Принимая во внимание соотношение между напряжением и током для катушки индуктивности (рис. 6)
, т.е. кривая напряжения искажена больше, чем кривая тока. Этому случаю будет соответствовать рис. 5 при взаимной замене на нем кривых напряжения и тока. Таким образом, катушка индуктивности является сглаживающим элементом для тока.