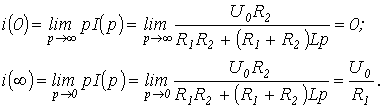 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Переход от изображений к оригиналам
Переход от изображения искомой величины к оригиналу может быть осуществлен следующими способами:
1. Посредством обратного преобразования Лапласа
,
которое представляет собой решение интегрального уравнения (1) и сокращенно записывается, как:
.
На практике этот способ применяется редко.
2. По таблицам соответствия между оригиналами и изображениями
В специальной литературе имеется достаточно большое число формул соответствия, охватывающих практически все задачи электротехники. Согласно данному способу необходимо получить изображение искомой величины в виде, соответствующем табличному, после чего выписать из таблицы выражение оригинала.
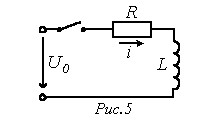Например, для изображения тока в цепи на рис. 5 можно записать
.
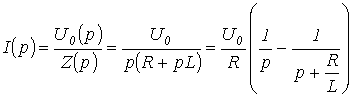Тогда в соответствии с данными табл. 1
,
что соответствует известному результату.
3. С использованием формулы разложения
Пусть изображение 
искомой переменной определяется отношением двух полиномов
,
где 
.
Это выражение может быть представлено в виде суммы простых дробей
 ,
| (3) |
где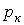 
- к-й корень уравнения 
.
Для определения коэффициентов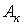 
умножим левую и правую части соотношения (3) на (
):
.
При 
.
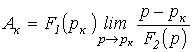Рассматривая полученную неопределенность типа 
по правилу Лапиталя, запишем
.
Таким образом,
.
Поскольку отношение 
есть постоянный коэффициент, то учитывая, что 
, окончательно получаем
 .
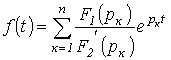| (4) |
Соотношение (4) представляет собой формулу разложения. Если один из корней уравнения равен нулю, т.е. 
, то уравнение (4) сводится к виду
.
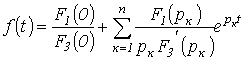В заключение раздела отметим, что для нахождения начального 
и конечного 
значений оригинала можно использовать предельные соотношения
которые также могут служить для оценки правильности полученного изображения.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Контрольные вопросы
- В чем заключается сущность расчета переходных процессов операторным методом?
- Что такое операторная схема замещения?
- Как при расчете операторным методом учитываются ненулевые независимые начальные условия?
- Какими способами на практике осуществляется переход от изображения к оригиналу?
- Для чего используются предельные соотношения?
- Как связаны изображение и оригинал в формуле разложения? Какие имеются варианты ее написания?
-
С использованием теоремы об активном двухполюснике записать операторное изображение для тока через катушку индуктивности в цепи на рис. 6.
Ответ: 
.
- С использованием предельных соотношений и решения предыдущей задачи найти начальное и конечное значения тока в ветви с индуктивным элементом.
Ответ: 
.
для перехода от комплекса к функции времени от правой части формулы разложения берется мнимая часть, т.е. выражение при j. Если при этом в цепи также имеют место другие источники, например, постоянной Е и экспоненциальной 
ЭДС, и начальные условия для токов в ветвях с индуктивными элементами и напряжений на конденсаторах ненулевые, то они должны быть все введены в формулу предварительно умноженными на j, поскольку только в этом случае они будут учтены при взятии мнимой части от формулы разложения, т.е. 
.
. Для сложных схем такое ее вычисление может оказаться достаточно трудоемким, в связи с чем принужденную составляющую в этих случаях целесообразно определять отдельно символическим методом, а свободную – операторным. 
.
Последовательность расчета переходных процессов операторным методом
1. Определение независимых начальных условий путем расчета докоммутационного режима работы цепи.
2. Составление операторной схемы замещения цепи (для простых цепей с нулевыми начальными условиями этот этап может быть опущен).
3. Запись уравнений по законам Кирхгофа или другим методам расчета линейных цепей в операторной форме с учетом начальных условий.
4. Решение полученных уравнений относительно изображений искомых величин.
5. 
Определение оригиналов (с помощью формулы разложения или таблиц соответствия оригиналов и изображений) по найденным изображениям.
В качестве примера использования операторного метода определим ток через катушку индуктивности в цепи на рис. 1.
С учетом нулевого начального условия операторное изображение этого тока
.
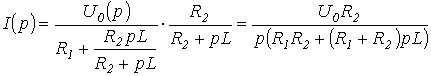Для нахождения оригинала 
воспользуемся формулой разложения при нулевом корне
,
, 
.
.
.
.
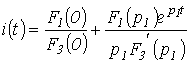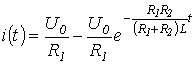и 
: