Уравнения линии конечной длины

Постоянные и 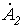в полученных в предыдущей лекции формулах

;

(5)

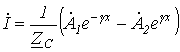
(6)

определяются на основании граничных условий.

Пусть для линии длиной l (см. рис. 1) заданы напряжение и ток в начале линии, т.е. при .

Тогда из (5) и (6) получаем

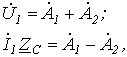
откуда

Подставив найденные выражения и 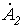в (5) и (6), получим

(7)

(8)

Уравнения (7) и (8) позволяют определить ток и напряжение в любой точке линии по их известным значениям в начале линии. Обычно в практических задачах бывают заданы напряжение и ток в конце линии. Для выражения напряжения и тока в линии через эти величины перепишем уравнения (5) и (6) в виде

;

(9)

.

(10)

Обозначив и , из уравнений (9) и (10) при получим

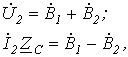
откуда

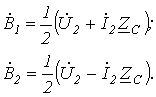
После подстановки найденных выражений и в (9) и (10) получаем уравнения, позволяющие определить ток и напряжение по их значениям в конце линии

;

(11)

.

(12)

Поиск по сайту: