АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Параллельное соединение резистивного и индуктивного элементов

Читайте также:
  1. B) Параллельное расположение показателей
  2. Алгоритмы упорядочивания элементов в массивах
  3. Бессоюзное соединение предложений
  4. Биогеохимические круговороты основных химических элементов в биосфере
  5. В зависимости от наличия тех или иных морфологических элементов сыпи выделяют различные типы дермального ангиита.
  6. Влияние легирующих элементов на превращение переохлажденного аустенита.
  7. Влияние легирующих элементов на структуру и механические свойства сталей
  8. Влияние элементов на полиморфизм железа
  9. Внешняя политика Ивана Грозного. Присоединение Башкирии к Русскому государству.
  10. Внешняя среда организации: значение, определение, взаимосвязь элементов.
  11. Возможности использования элементов налоговой политики и налогового учета организации для целей оптимизации налоговых потоков
  12. Вопрос№36 Последовательное и параллельное соединение проводников

Для цепи на рис. 21 можно записать

;

, где [См] – активная проводимость;

, где [См] – реактивная проводимость катушки индуктивности.

Векторной диаграмме токов (рис. 22) для данной цепи соответствует уравнение в комплексной форме

,

где ;

- комплексная проводимость;

.

Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 23.

 
 


Выражение комплексного сопротивления цепи на рис. 21 имеет вид:

.

Литература

1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1. В чем сущность реактивных сопротивлений?

2. Какой из элементов: резистор, катушку индуктивности или конденсатор – можно использовать в качестве шунта для наблюдения за формой тока?

3. Почему катушки индуктивности и конденсаторы не используются в цепях постоянного тока?

4. В ветви на рис. 12 . Определить комплексное сопротивление ветви, если частота тока .
Ответ: .

5. В ветви на рис. 15 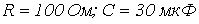. Определить комплексное сопротивление ветви, если частота тока .
Ответ: .

6. В цепи на рис. 18 . Определить комплексные проводимость и сопротивление цепи для .
Ответ: ; .

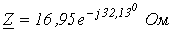7. Протекающий через катушку индуктивности ток изменяется по закону А. Определить комплекс действующего значения напряжения на катушке.
Ответ: .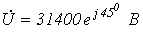
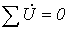
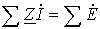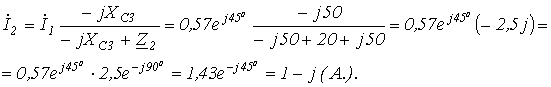
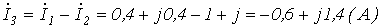Лекция N 5. Закон Ома для участка цепи с источником ЭДС.

 

 
 


Возьмем два участка цепи a-b и c-d (см. рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на рис. 1 положительных направлений напряжений и токов.

Объединяя оба случая, получим

(1)

или для постоянного тока

. (2)

 

Формулы (1) и (2) являются аналитическим выражением закона Ома для участка цепи с источником ЭДС, согласно которому ток на участке цепи с источником ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной на сопротивление участка. В случае переменного тока все указанные величины суть комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление совпадает с выбранным направлением тока, и со знаком “-”, если их направление противоположно направлению тока.

 

Основы символического метода расчета цепей
синусоидального тока

 

Расчет цепей переменного синусоидального тока может производиться не только путем построения векторных диаграмм, но и аналитически – путем операций с комплексами, символически изображающими синусоидальные ЭДС, напряжения и токи. Достоинством векторных диаграмм является их наглядность, недостатком – малая точность графических построений. Применение символического метода позволяет производить расчеты цепей с большой степенью точности.

Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной форме.

Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин.

1. Первый закон Кирхгофа в комплексной форме:

. (3)

 

2. Второй закон Кирхгофа в комплексной форме:

(4)

 

или применительно к схемам замещения с источниками ЭДС

. (5)

 

3. Соответственно матричная запись законов Кирхгофа в комплексной форме имеет вид:

§ первый закон Кирхгофа:

. ; (6)

 

§ второй закон Кирхгофа

. (7)

 

Пример.

Дано:

Определить: 1) полное комплексное сопротивление цепи ;  
2) токи  
Рис. 2  

Решение:

 

1. .

2. .

3.

.

4. Принимая начальную фазу напряжения за нуль, запишем:

.

Тогда

.

5. Поскольку ток распределяется обратно пропорционально сопротивлению ветвей (это вытекает из закона Ома), то

6. .

7. Аналогичный результат можно получить, составив для данной схемы уравнения по законам Кирхгофа в комплексной форме

или после подстановки численных значений параметров схемы

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)