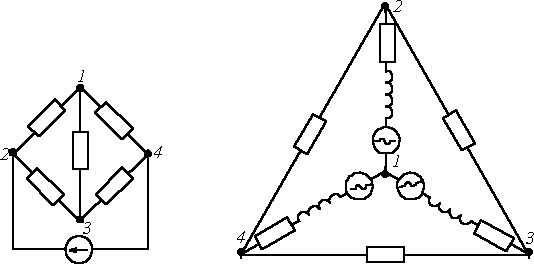
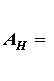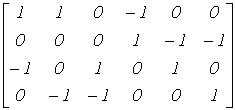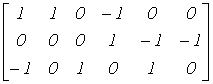Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. Рассмотрим для примера две электрические схемы (рис. 1, 2), введя понятие ветви и узла.
Ветвью называется участок цепи, обтекаемый одним и тем же током.
Узел – место соединения трех и более ветвей.
Представленные схемы различны и по форме, и по назначению, но каждая из указанных цепей содержит по 6 ветвей и 4 узла, одинаково соединенных. Таким образом, в смысле геометрии (топологии) соединений ветвей данные схемы идентичны.
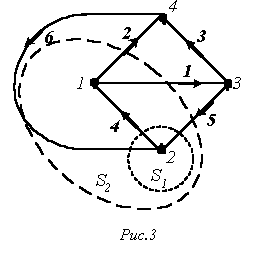 Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3. Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3.
Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, называется графом электрической цепи. При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом.
Отрезок линии, соответствующий ветви схемы, называется ветвью графа. Граничные точки ветви графа называют узлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называется ориентированным.
Подграфом графа называется часть графа, т.е. это может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе.
В теории электрических цепей важное значение имеют следующие подграфы:
1. Путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются на этом пути только один раз. Например, в схеме на рис. 3 ветви 2-6-5; 4-5; 3-6-4; 1 образуют пути между одной и той же парой узлов 1 и 3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно.
2. Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. Например, для графа по рис. 3 можно определить контуры, образованные ветвями 2-4-6; 3-5-6; 2-3-5-4. Если между любой парой узлов графа существует связь, то граф называют связным.
3. Дерево – это связный подграф, содержащий все узлы графа, но ни одного контура. Примерами деревьев для графа на рис. 3 могут служить фигуры на рис. 4.
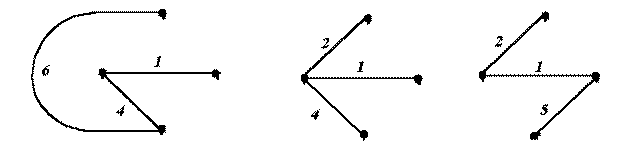
Рис.4
4. Ветви связи (дополнения дерева) – это ветви графа, дополняющие дерево до исходного графа.
Если граф содержит m узлов и n ветвей, то число ветвей любого дерева  , а числа ветвей связи графа , а числа ветвей связи графа  . .
5. Сечение графа – множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых, в частности, может быть отдельным узлом.
Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности, рассекающей соответствующие ветви. Примерами таких поверхностей являются для нашего графа на рис. 3 S1 и S2. При этом получаем соответственно сечения, образованные ветвями 6-4-5 и 6-2-1-5.
С понятием дерева связаны понятия главных контуров и сечений:
- главный контур – контур, состоящий из ветвей дерева и только одной ветви связи;
- главное сечение – сечение, состоящее из ветвей связи и только одной ветви дерева.
Топологические матрицы
Задать вычислительной машине топологию цепи рисунком затруднительно, так как не существует эффективных программ распознавания образа. Поэтому топологию цепи вводят в ЭВМ в виде матриц, которые называют топологическими матрицами. Выделяют три таких матрицы: узловую матрицу, контурную матрицу и матрицу сечений.
1. Узловая матрица (матрица соединений) – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа. Строки этой матрицы соответствуют узлам, а столбцы – ветвям схемы.
Для графа на рис. 3 имеем число узлов m=4 и число ветвей n=6. Тогда запишем матрицу АН, принимая, что элемент матрицы 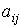 (i –номер строки; j –номер столбца) равен 1, если ветвь j соединена с узлом i и ориентирована от него, -1, если ориентирована к нему, и 0, если ветвь j не соединена с узлом i. Сориентировав ветви графа на рис. 3, получим (i –номер строки; j –номер столбца) равен 1, если ветвь j соединена с узлом i и ориентирована от него, -1, если ориентирована к нему, и 0, если ветвь j не соединена с узлом i. Сориентировав ветви графа на рис. 3, получим
.Данная матрица АН записана для всех четырех узлов и называется неопределенной. Следует указать, что сумма элементов столбцов матрицы АН всегда равна нулю, так как каждый столбец содержит один элемент +1 и один элемент -1, остальные нули.
Обычно при расчетах один (любой) заземляют. Тогда приходим к узловой матрице А (редуцированной матрице), которая может быть получена из матрицы АН путем вычеркивания любой ее строки. Например, при вычеркивании строки “4” получим
.Число строк матрицы А равно числу независимых уравнений для узлов  , т.е. числу уравнений, записываемых для электрической схемы по первому закону Кирхгофа. Итак, введя понятие узловой матрицы А, перейдем к первому закону Кирхгофа. , т.е. числу уравнений, записываемых для электрической схемы по первому закону Кирхгофа. Итак, введя понятие узловой матрицы А, перейдем к первому закону Кирхгофа.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | Поиск по сайту:
|


 Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3.
Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3.
 , а числа ветвей связи графа
, а числа ветвей связи графа  .
.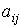 (i –номер строки; j –номер столбца) равен 1, если ветвь j соединена с узлом i и ориентирована от него, -1, если ориентирована к нему, и 0, если ветвь j не соединена с узлом i. Сориентировав ветви графа на рис. 3, получим
(i –номер строки; j –номер столбца) равен 1, если ветвь j соединена с узлом i и ориентирована от него, -1, если ориентирована к нему, и 0, если ветвь j не соединена с узлом i. Сориентировав ветви графа на рис. 3, получим