АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Б) Відношення еквівалентності

Читайте также:
  1. Апочаткування позитивістської філософії у XIX ст. та її відношення до метафізики. Погляди О.Конта та Г.Спенсера.
  2. Б) суттєве, закономірне відношення і взаємодія між протилежними
  3. В) відношення затрат ресурсів на виробництво певної кількості про-
  4. Види інноваційних стратегій та їх співвідношення
  5. Використання логічних операторів та операторів співвідношення
  6. Відношення між величинами
  7. Відношення між поняттями
  8. Відношення між РЕ і Р - маршрутизаторами
  9. За допомогою рівнянь (V.3.1) і (V.4.5) одержимо співвідношення
  10. Закон в англійській правовій системі. Співвідношення закону і прецеденту
  11. Західноєвропейська теологія про співвідношення культури й релігії

Відношення 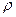називається відношенням еквівалентності, якщо воно рефлексивне, симетричне і транзитивне.

Приклади.

1. Відношення рівності.

2. Відношення подібності трикутників.

Розбиттям непорожньої множини А називається сукупність 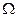непорожніх підмножин Х множини А таких, що:

1. 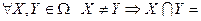ø.

2. Об’єднання всіх підмножин Х множини А дорівнює множині А.

Якщо 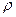– відношення еквівалентності на множині А, то можна утворити розбиття 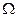множини А на класи еквівалентних елементів так, щоб для будь-яких , які належать до одного класу, справджувалось , а для будь-яких , які належать до різних класів, справджувалось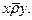

Приклади.

1. Відношення еквівалентності 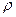– „бути подібним” розбиває множину всіх трикутників площини на класи подібних між собою трикутників.

2. Відношення еквівалентності 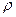– „навчатися в одній групі” розбиває множину студентів факультету на класи еквівалентності – академічні групи.

 


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)