Контрольная работа №2

161 - 180. Найти общее решение дифференциального уравнения.

161. 162.

163. 164.

165. 166.

167. 168.

169. 170.

171. 172.

173. 174.

175. 176.

177. 178.

179. 180.

В задачах 181 - 200 даны дифференциальные уравнения второго порядка, допускающие понижение порядка. Найти частное решение, удовлетворяющее указанным начальным условиям.

181. у΄΄- е^уу΄= 0, у(0) = 0, у΄(0) = 1.

182. у΄у΄΄= 2у, у(0) = 0, у΄(0) = 0.

183. уу΄΄= (у΄)², у(0) = 1, у΄(0) = 3.

184. у³у΄΄= 3, у(1) = 1, у΄(1) = 1.

185. у΄΄-12у²= 0, у(0) =1/2, у΄(0) = 1.

186. 2у΄΄=е^4у, у(0) = 0, у΄(0) = ½.

187. (у – 2)у΄΄ = 2(у΄)², у(0) = 3, у΄(0) = 1.

188. 2уу΄΄= 3 + (у΄)², у(1) = 1, у΄(1) = 1.

189. у΄΄= у(2) = 0, у΄(2) = 2.

190. (у + 1)²у΄΄= (у΄)³, у΄(0) = 1.

191.

192.

193.

194.

195.

196.

197.

198.

199.

200.

201 - 220. Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям у(0)=у₀,

201.

202.

203.

204.

205.

206.

207.

208.

209.

210.

211. y΄΄-2y΄-8y=16x²+2, y(0)=0, y΄(0)=5.

212. y΄΄+4y=3cos x, y(0)=1, y΄(0)=2.

213. y΄΄-y΄-2y=3e^2x, y(0)=2, y΄(0)=5.

214. y΄΄-2y΄=2x+1, y(0)=1, y΄(0)=1.

215. y΄΄-2y΄+y=9e^-2x+2x-4, y(0)=1, y΄(0)=1.

216. y΄΄-4y=4sin 2x, y(0)=2, y΄(0)=7.

217. y΄΄+y΄=3cos x – sin x, y(0)=0, y΄(0)=1.

218. y΄΄-y΄-6y=6x²-4x-3, y(0)=3, y΄(0)=5.

219. y΄΄-3y΄=3e^3x, y(0)=2, y΄(0)=4.

220. y΄΄-4y΄+5y=5x – 4, y(0)=0, y΄(0)=3.

221. Вычислить площадь фигуры, ограниченной параболами и .

222. Вычислить площадь фигуры, ограниченной эллипсом x = acos t, y = bsint.

223. Вычислить площадь фигуры, ограниченной астроидой x = 4cos³t, y = 4sin³t.

224. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболой , х = 4 и осью Ох.

225. Найти объем тела, полученного вращением вокруг оси Оу фигуры, ограниченной гиперболой у = 6/х, осью Оу и прямыми у = 1 и у = 6.

226. Найти объем тела, полученного вращением вокруг оси Ох эллипса

х = аcost, y = bsint.

227. Найти длину дуги кривой от х₁ = 0 до х₂ = 12.

228. Найти длину дуги кривой у = lnx от х₁= ¾ до х₂ = 2,4.

229. Найти длину одной арки циклоиды х = а(t - sint), y = a(1-cost).

230. Найти длину кардиоиды r = 2a(1-cosφ).

231 – 240. Найти площадь фигуры, ограниченной данными линиями.

231.

232.

233.

234.

235.

236.

237.

238.

239.

240.

241 - 260. Исследовать сходимость числового ряда.

241. 242.

243. 244.

245. 246.

247. 248.

249. 250.

251. . 252. .

253. . 254. .

255. 256. .

257. . 258. .

259. . 260.

261 - 280. Найти интервал сходимости степенного ряда.

261. 262.

263. 264.

265. 266.

267. 268.

269. 270.

271. . 272. .

273. . 274. .

275. . 276. .

277. . 278. .

279. . 280. .

281 - 300. Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в ряд и затем проинтегрировав его почленно.

281. 282

283. 284.

285. 286.

287. 288.

289. 290.

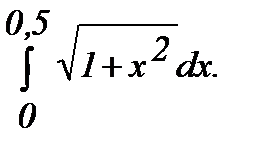
291. . 292. .

293. . 294. .

295. . 296. .

297. 298. .

299. . 300. .

301. Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что: а) студент знает все три вопроса; б) только два вопроса; в) только один вопрос экзаменационного билета.

302. В каждой из двух урн находятся 5 белых и 10 черных шаров. Из первой урны во вторую переложили неудачу один шар, а затем из второй урны вынули наугад один шар. Найти вероятность того, что вынутый шар окажется черным.

303. Три стрелка в одинаковых и независимых условиях производили по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 0,9, вторым – 0,8, третьим – 0,7. Найти вероятность того, что: а) только один из стрелков попадает в цель; б) только два стрелка попадут в цель; в) все три стрелка попадут в цель.

304. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Найти вероятность того, что в 1600 испытаниях событие наступит 1200 раз.

305. Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равна 0,9, второе – 0,95, третье – 0,85. Найти вероятность того, что при аварии сработает: а) только одно устойство; б) только два устройства; в) все три устройства.

306. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,02. Найти вероятность того, что в 150 испытаниях событие наступит 5 раз.

307. В партии из 1000 изделий имеются 10 дефектных. Найти вероятность того, что среди 50 изделий, наудачу взятых из этой партии, ровно три окажутся дефектными.

308. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Найти вероятность того, что в 125 испытаниях событие наступит не менее 75 и не более 90 раз.

309. На трех станках при одинаковых и независимых условиях изготовляют детали одного наименования. На первом станке изготовляют 10%, на втором – 30, на третьем – 60% всех деталей. Вероятность каждой детали быть бездефектной равна 0,7, если она изготовлена на первом станке, 0,8, - если на втором станке, и 0,9, - если на третьем станке. Найти вероятность того, что наугад взятая деталь окажется бездефектной.

310. Два брата входят в состав двух спортивных команд, состоящих из 12 человек каждая. В двух урнах имеются по 12 билетов с номерами от 1до 12. Члены каждой команды вынимают наудачу по одному билету из определенной урны (без возвращения). Найти вероятность того, что оба брата вытащат билет номер 6.

311. В цехе 6 моторов. Для каждого мотора вероятность того, что в данный момент включен равна 0,8. Найти вероятность того, что в данный момент:

а) включено 4 мотора;

б) выключены все моторы;

в) включены все моторы;

г) включен хотя бы один мотор.

312. Монету бросают 5 раз. Найти вероятность того, что герб выпадет:

а) 3 раза;

б) не менее 3-х раз;

в) не более 3-х раз;

г) хотя бы 1 раз.

313. Для прядения смешивают поровну белый и окрашенный хлопок. Какова вероятность того, что среди 5 случайно выбранных волокон обнаружится:

а) ровно 2 окрашенных;

б) менее 2 окрашенных;

в) более 2 окрашенных;

г) хотя бы 4 окрашенных.

314. Средний процент нарушения кинескопа телевизора в течение гарантийного срока равен 12. Вычислить вероятность того, что из 10 наблюдаемых телевизоров гарантийный срок выдержат:

а) 8 телевизоров;

б) не менее 8 телевизоров;

в) хотя бы 1 телевизор.

315. Наблюдениями установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность того, что из случайно взятых в этом месяце 8 дней дождливыми окажутся:

а) ровно 3 дня;

б) не более 3-х дней;

в) хотя бы 1 день.

316. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двух и более пуль, если число выстрелов равно 5000.

317. Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна 0,01. Телефонная станция обслуживает 800 абонентов. Какова вероятность того, что в течение часа позвонят:

а) 5 абонентов;

б) хотя бы 1 абонент.

318. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение одной минуты равна 0,004. Какова вероятность того, что в течение одной минуты обрыв произойдет на:

а) 5 веретенах;

б) не менее, чем на 1 веретене.

319. Производство дает 1% брака. Какова вероятность того, что из взятых на исследование 1100 изделий выбраковано будет не более 2-х.

320. Семена пшеницы содержат 0,3% сорняков. Найти вероятность того, что в 1000 семян будет:

а) ровно 5;

б) хотя бы 2 сорняка.

321 - 340. Задан закон распределения случайной величины X – размер деталей, выпускаемых заводом (в первой строке таблицы даны возможные значения измеренной детали, а во второй строке указаны вероятности p этих возможных значений).

Найти: 1) математическое ожидание M(X); 2) дисперсию D(X); 3) среднее квадратическое отклонение .

Поиск по сайту: