 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Функциональные и степенные ряды
Пример 2. Найти область сходимости степенного ряда: 
Решение
а) Данный степенной ряд можно записать так:
Применяем признак Даламбера и ищем предел:
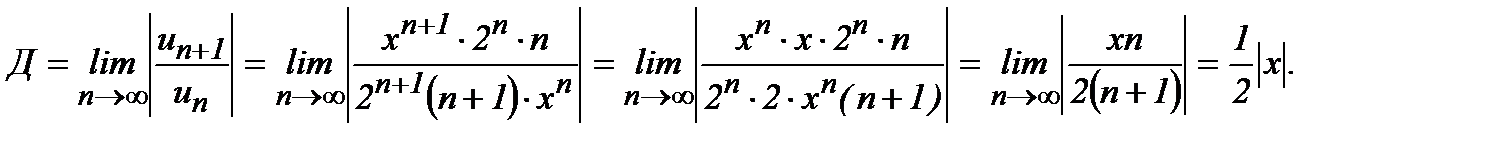
Как видно, ряд будет сходиться для тех значений х, для которых 
Таким образом, интервал сходимости данного ряда (-2; 2). Граничные точки интервала сходимости х = 
2, для которых Д = 1 и признак Даламбера не решает вопроса о сходимости ряда, и исследуется особо.
При х = -2, получим числовой знакочередующийся ряд 
для которого выполняются все условия признака Лейбница: 
и 
Следовательно ряд сходится. При х = 2, получим гармоничный ряд 
который расходится.
Следовательно, областью сходимости данного ряда является полуоткрытый интервал:
-2 ≤ х < 2
б) Здесь 
Применим признак Коши, находя предел:
при любом х ≠ 0.
Следовательно, заданный степенной ряд расходится при всех значениях х ≠ 0 и сходится только при х = 0.
Пример 3. Вычислить интеграл 
с точностью до 0,001.
Решение
Предварительно представим подынтегральную функцию в виде степенного ряда. Используя известное разложение в степенной ряд функции sin x, имеем:
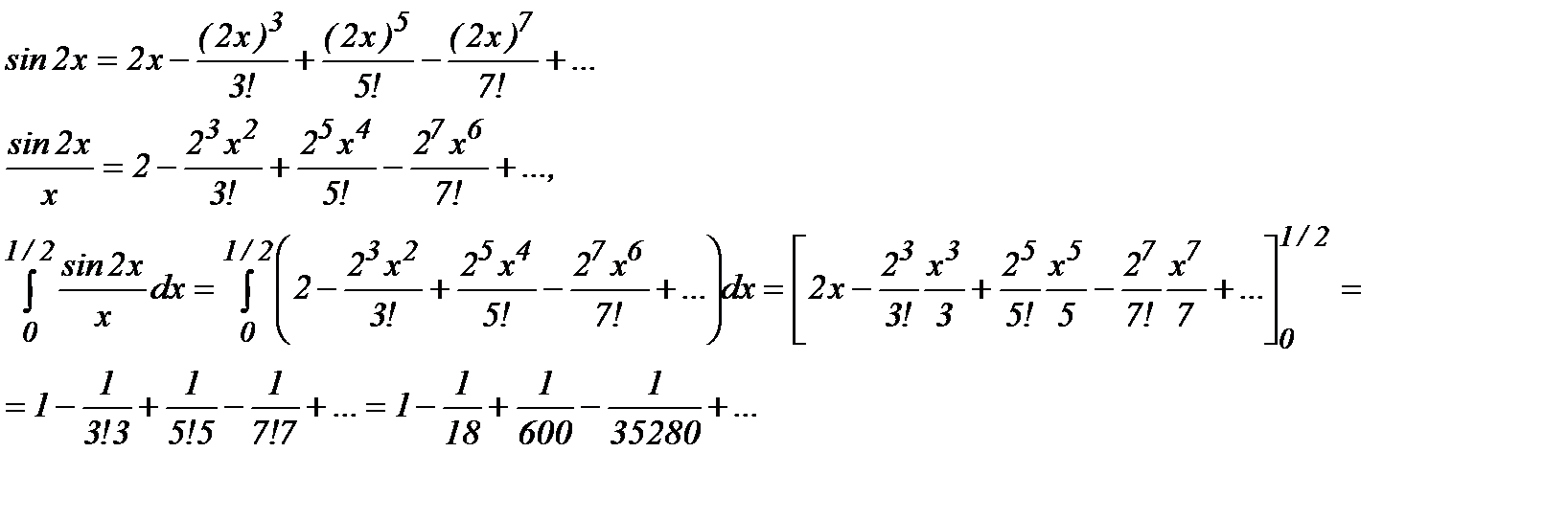
Получен знакочередующийся ряд, который удовлетворяет условиям теоремы Лейбница. Так как в этом ряде четвертый член по абсолютному значению меньше 0,001, то ограничимся только первыми тремя членами. Итак,
Пример 4. Найти первые три (отличные от нуля) члена разложения в ряд Маклорена функции у(х), являющейся частным решением дифференциального уравнения у΄ = х + х2-у2+ cos x, если у(0)=1.
Решение
Положим, что у(х) является решением данного дифференциального уравнения при указанных начальных условиях. Если функцию у(х) можно разложить в ряд Маклорена, то
(1)
Свободный член разложения (1), т.е у(0), дан по условию. Чтобы найти значения у΄(0), у΄΄(0),
у΄΄΄(0), …, можно данное уравнение последовательно дифференцировать по переменной х и затем вычислить значения производных при х=0.
Значение у΄(0) получаем, подставив начальные условия в данное уравнение:
Подставив найденные значения производных при х=0 в (1), получим разложение искомого частного решения заданного уравнения:
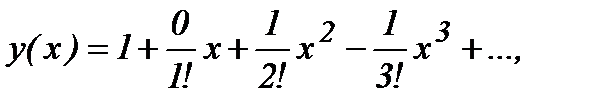или
Поиск по сайту: