Применяя формулу (1), получим

Следовательно,

4) Площадь грани А₁ А₂ А₃ равна половине площади параллелограмма, построенного на векторах и . Обозначим через вектор 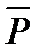векторное произведение векторов и 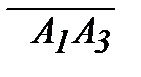, тогда площадь параллелограмма , а площадь грани

Координаты вектора найдем по формуле (3):

(11; 2; 10)

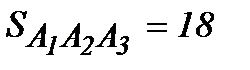кв. ед.

5) Объем пирамиды V в шесть раз меньше объема параллелепипеда V₁, построенного на трех некомпланарных векторах, и равен абсолютной величине их смешанного произведения. Вычислим смешанное произведение :

Следовательно, V₁ параллелепипеда равен 144 куб. ед., а объем заданной пирамиды V = 144/6 =24 куб. ед.

6) Уравнение прямой, проходящей через две заданные точки А₁ (х₁, y₁, z₁) и А₂ (х₂, y₂, z₂) имеет вид

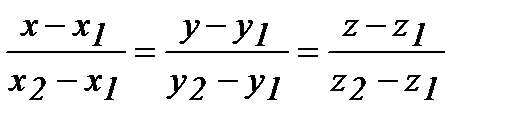(7)

Подставив в (7) координаты точек А₁ и А₂, получим

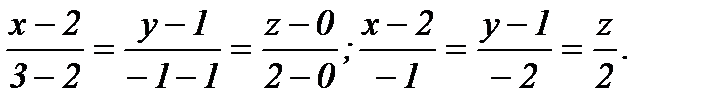
7) Уравнение плоскости А₁А₂А₃ – это уравнение грани А₁А₂А₃, которое найдено в п.3:

А₁А₂А₃ : 2х – у – 2z – 3 = 0

8) Уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃ – это перпендикуляр А₄Д. Каноническое уравнение прямой в пространстве имеет вид

(8)

где х₀, у₀, z₀ – координаты точки, через которую проходит прямая (8), а m, n, p – направляющие коэффициенты этой прямой. По условию прямая проходит через точку А₄( 0; 1; 4) и перпендикулярные грани А_!А₂А₃ для которой (2; -1; -2), т.е. подставив эти данные в формулу (8), получаем

- уравнение высоты А₄Д

Пример 3. Данную систему уравнений:

решить по формулам Крамера (через определитель) и средствами матричного исчисления (с помощью обратной матрицы).

Решение.

Обозначим через А матрицу коэффициентов при неизвестных;

Х – матрицу - столбец неизвестных х₁, х₂, х₃;

В – матрицу – столбец свободных членов:

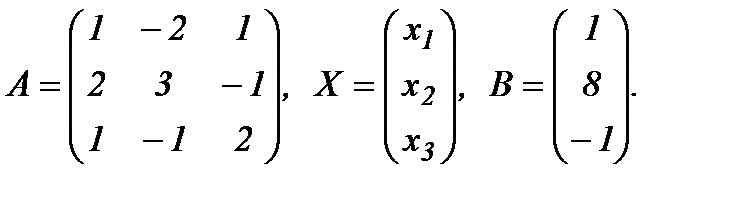
С учетом этих обозначений данная система уравнений примет следующую матричную форму:

(1)

Если матрица А – невырожденная (ее определитель ), то она имеет обратную матрицу А^-1. умножив обе части уравнения (1) на А^-1, получим:

,

но - единичная матрица, а ЕХ = Х, поэтому

(2)

Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо выписать обратную матрицу А^-1.

Пусть имеем невырожденную матрицу и ее определитель равен Δ, тогда где A_ij (i = 1,2,3; j = 1,2,3) – алгебраическое дополнение элемента a_ij в определителе матрицы А и

где M_ij – минор (определитель) второго порядка, полученный вычеркиванием i –й строки и j – го столбца в определителе матрицы А.

Вычислим определитель Δ и алгебраические дополнения A_ij элементов матрицы А.

следовательно матрица А невырожденная и имеет обратную матрицу А ^-1.

тогда

По формуле (2) находим решение данной системы уравнений в матричной форме:

отсюда х₁=3, х₂=0, х₃=-2.

Если определитель системы уравнений то такая система уравнений имеет одно определенное решение, получаемое по формулам

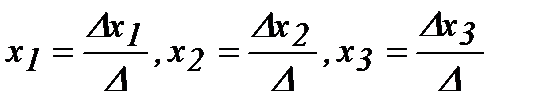(3)

Формулы (3) называются формулами Крамера, где Δх_i получается заменой i-го столбца в главном определителе Δ столбцом свободных членов.

Если определитель системы Δ=0 и по крайней мере один из определителей , то такая система уравнений не имеет решения. Если же Δ=0 и все Δх_i=0, то данная система уравнений либо не имеет решения, либо имеет бесчисленное множество решений.

Определитель данной системы .

Вычислим вспомогательные определители:

Применяя формулы (3), находим:

Пример 4. Решить систему методом Гаусса

Решение.

Составим по данной системе расширенную матрицу

умножим первую строку на и сложим со второй строкой и с четвертой строкой; умножим первую строку на и сложим с третьей строкой, получим

поменяем местами вторую и третью строки

умножим вторую строку на 7 и сложим с четвертой строкой

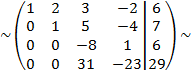
умножим третью строку на 31, а четвертую на 8 и сложим эти строки

разделим последнюю строку на 2

От ступенчатого вида матрицы переходим к системе

т.е. обратным ходом Гаусса находим все переменные.

Поиск по сайту: