Числовые ряды. Пусть и1, и2, , иn, , где иn= f(n) – бесконечная числовая последовательность

Пусть и₁, и₂, …, и_n, …, где и_n= f(n) – бесконечная числовая последовательность. Выражение

и₁+ и₂+ и₃ + …+ и_n+ …

называется бесконечным числовым рядом, а числа и₁, и₂, …, и_n – членами ряда; и_n = f(n) – называется общим членом. Ряд часто записывают в виде:

Перечислим важнейшие признаки сходимости и расходимости рядов с положительными членами.

Необходимый признак сходимости ряда. Если ряд и₁+ и₂+ и₃ + …+ и_n+ … сходится, то т.е. при n→∞ предел общего члена сходящегося ряда равен нулю. Таким образом, если то ряд расходится.

Первый признак сравнения. Пусть даны два ряда

и₁+ и₂+ и₃ + …+ и_n+ … (1)

σ₁+ σ₂+ σ₃ + …+ σ_n+ …, (2)

причем каждый член ряда (1) не превосходит соответствующего члена ряда (2), т.е. и_n≤ σ_n (n = 1, 2, 3, …). Тогда если сходится ряд (2), то сходится и ряд (1); если расходится ряд (1), то расходится и ряд (2).

Второй признак сравнения. Если существует конечный и отличный от нуля предел 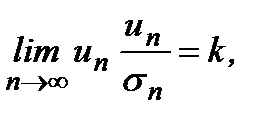то оба ряда и одновременно сходятся или одновременно расходятся.

Признак Коши. Если для ряда (1) существует то этот ряд сходится при С < 1 и расходится при С > 1.

Признак Даламбера. Если для ряда (1) существует то этот ряд сходится при Д <1 и расходится при Д >1.

Интегральный признак. Если f(x) при х ≥ 1 – непрерывная, положительная и монотонно убывающая функция, то ряд , где и_n=f(n), сходится или расходится в зависимости от того, сходится или расходится интеграл (N ≥1).

Знакопеременные ряды

Ряд, члены которого имеют чередующиеся знаки, называют знакочередующимися:

и₁- и₂+ и₃ – и₄+ …+(-1)ⁿ⁺¹ и_n+ …,

где u_n>0 (n = 1, 2, 3, …).

Признак сходимости знакочередующегося ряда (признак Лейбница).

Знакочередующийся ряд сходится, если абсолютная величина его членов монотонно убывает, а общий член стремится к нулю, т.е. если выполняется следующее условие:

1 ) и₁> и₂> и₃ > …

и

2)

Пример 1. Исследовать сходимость числового ряда;

а)

б)

Решение

а) применим признак Даламбера. Выпишем n -ый и (n + 1) – ый члены ряда:

Тогда

и данный ряд сходится.

б) Применим интегральный признак: ; следовательно, - непрерывная, положительная и монотонно убывающая функция при х ≥ 1 и

Данный интеграл – сходящийся, поэтому сходится и исследуемый ряд.

Поиск по сайту: