 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Исследование функций и построение графиков
Вычисление пределов функций.
Найти пределы.
1. 
2. 
3. 
4. 
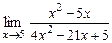
5. 
6. 
7. 
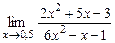
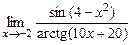
8. 
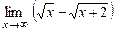
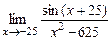
9. 
10. 
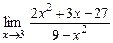
11. 
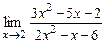
12. 
13. 
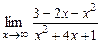
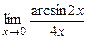
14. 
15. 
16. 
17. 
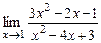
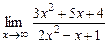
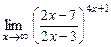
18. 
19. 
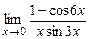
20. 
21. 
22. 
23. 
24. 
25. 
26. 
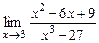
27. 
28. 
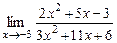
29. 
30. 
Исследовать точки разрыва функции.
Функция 
задана различными выражениями для различных областей изменения аргумента 
.
Требуется:
1. найти точки разрыва функции, если они существуют;
2. найти односторонние пределы и скачок функции в точках разрыва;
3. построить график функции.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
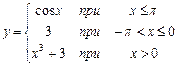
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
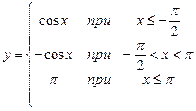
24. 
25. 
26. 
27. 
28. 
29. 
30. 
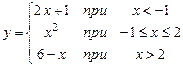
Вычислить производные функции.
Найти производные функций, пользуясь правилами дифференцирования.
1. 
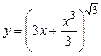
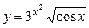
2. 
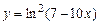
3. 
4. 
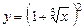
5. 
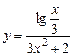
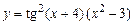
6. 
7. 
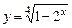
8. 
9. 
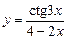
10. 
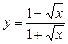
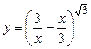
11. 
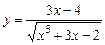
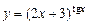
12. 
13. 
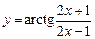
14. 
15. 
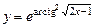
16. 
17. 
18. 
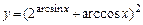
19. 
20. 
21. 
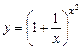
22. 
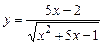
23. 
24. 
25. 
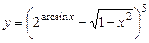
26. 
27. 
28. 
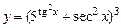
29. 
30. 
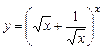
Вычисление производных неявных функций.
Найти производные первого и второго порядков для функций, заданных неявно.
1. 
2. 
3. 
4. 
5. 
6. 
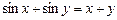
7. 
8. 
9. 
10. 
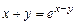
11. 
12. 
13. 
14. 
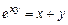
15. 
16. 
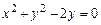
17. 
18. 
19. 
20. 
21. 
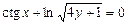
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
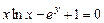
Вычисление производных параметрических функций.
Найти производные первого и второго порядков для функций, заданных параметрически.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
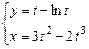
11. 
12. 
13. 
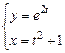
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
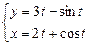
22. 
23. 
24. 
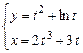
25. 
26. 
27. 
28. 
29. 
30. 
Применение дифференциалов в приближенных вычисленниях.
Найти приближенное значение указанных величин с помощью дифференциалов соответствующих функций. Все вычисления выполнять с четырьмя десятичными знаками.
1. 
2. 
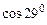
3. 
4. 
5. 
6. 
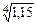
7. 
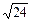
8. 
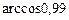
9. 
10. 
11. 
12. 
13. 
14. 
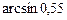
15. 
16. 
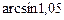
17. 
18. 
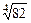
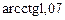
19. 
20. 
21. 
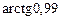
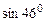
22. 
23. 
24. 
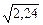
25. 
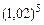
26. 
27.
28. 
29. 
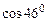
30.
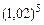
Вычисление пределов по правилу Лопиталя.
Вычислить пределы, используя правило Лопиталя.
1. 
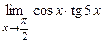
2. 
3. 
4. 
5. 
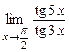
6. 
7. 
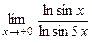
8. 
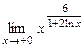
9. 
10. 
11. 
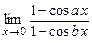
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
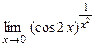
24. 
25. 
26. 
27. 
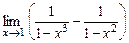
28. 
29. 
30. 
Исследование функций и построение графиков.
Исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование и построение графика рекомендуется проводить по следующей схеме:
1. найти область определения функции;
2. исследовать функцию на непрерывность; найти точки разрыва функции и ее односторонние пределы в этих точках;
3. выяснить, не является ли функция четной, нечетной или периодической;
4. найти точки пересечения графика функции с осями координат и интервалы знакопостоянства функции;
5. найти асимптоты графика функции: а) вертикальные и б) невертикальные;
6. найти точки экстремума и интервалы возрастания и убывания функции;
7. найти точки перегиба графика функции и интервалы выпуклости вверх и вниз;
8.построить график функции, используя все полученные результаты исследования; при необходимости можно дополнительно находить точки графика, задавая аргументу нужные значения и вычисляя соответствующие значения функции.
1. 
2. 
3. 
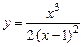
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
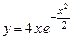
16. 
17. 
18. 
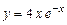
19. 
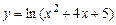
20. 
21. 
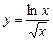
22. 
23. 
24. 
25. 
26. 
27. 
28. 
Поиск по сайту: