АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Тема 22. Интервальные оценки

Читайте также:
  1. III. Методы оценки функции почек
  2. Абсолютные показатели оценки риска
  3. Акционерное финансирование. Методы оценки стоимости акций.
  4. Алгоритм оценки и проверки адекватности нелинейной по параметрам модели (на примере функции Кобба-Дугласа).
  5. Биохимические методы исследования и оценки физической работоспособности
  6. В 3. Основные производственные фонды: экономическая сущность, классификация, виды оценки.
  7. В 3. Показатели оценки эффективности инвестиционных проектов.
  8. В чем заключается противоречие между несмещенностью и эффективностью оценки? Выбор наилучшей оценки.
  9. Виды оценки осн. фондов
  10. Виды работ, учитываемые при расчете оценки по модулю
  11. Вопрос: Методы оценки личных и деловых качеств персонала.
  12. Выписка из Методики оценки масштабов и последствий

1. Найти доверительный интервал для оценки с надежностью 0,99 неизвестного математического ожидания α нормально распределенного признака Х генеральной совокупности, если даны генеральное среднее квадратическое отклонение а, выборочная средняя 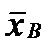и объем выборки n:

σ = 4, 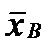= 10,2, n = 16.

Отв. 7,63 < α < 12,77.

 

2. Найти доверительный интервал для оценки с надежностью 0,99 неизвестного математического ожидания α нормально распределенного признака Х генеральной совокупности, если даны генеральное среднее квадратическое отклонение а, выборочная средняя 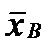и объем выборки n:

σ = 5, 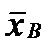= 16,8, n = 25.

Отв. 14,23 < α < 19,37.

 

3. Одним и тем же прибором со средним квадратическим отклонением случайных ошибок измерений σ = 40 м произведено 5 равноточных измерений расстояния от орудия до цели. Найти доверительный интервал для оценки истинного расстояния α до цели с надежностью ν = 0,95, зная среднее арифметическое результатов измерений 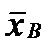= 2000 м.

Отв. 1960,8 < α < 2039,2.

 

4. Выборка из большой партии электроламп содержит 100 ламп. Средняя продолжительность горения лампы выборки оказалась равной 1000 ч. Найти с надежностью 0,95 доверительный интервал для средней продолжительности α горения лампы всей партии, если известно, что среднее квадратическое отклонение продолжительности горения лампы σ = 40 ч.

Отв. 992,16 < α < 1007,84.

 

5. Станок-автомат штампует валики. По выборке объема n = 100 вычислена выборочная средняя диаметров изготовленных валиков. Найти с надежностью 0,95 точность δ, с которой выборочная средняя оценивает математическое ожидание диаметров изготовляемых валиков, зная, что их среднее квадратическое отклонение σ = 2 мм.

Отв.

 

6. Найти минимальный объем выборки, при котором с надежностью 0,975 точность оценки математического ожидания α генеральной совокупности по выборочной средней будет равна δ = 0,3, если известно среднее квадратическое отклонение σ = 1,2 нормально распределенной генеральной совокупности.

Отв. N=81

 

7. Найти минимальный объем выборки, при котором с надежностью 0,925 точность оценки математического ожидания нормально распределенной генеральной совокупности по выборочной средней будет равна 0,2, если известно среднее квадратическое отклонение генеральной совокупности σ = 1,5.

Отв. n = 179.

 

8. Из генеральной совокупности извлечена выборка объема n = 10:

варианта xi -2          
частота ni            

Оценить с надежностью 0,95 математическое ожидание α нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интеграла.

Отв. 0,3 < α < 3,7

 

9. Из генеральной совокупности извлечена выборка объема n = 12:

варианта xi -0,5 -0,4 -0,2   0,2 0,6 0,8   1,2 1,5
частота ni                    

Оценить с надежностью 0,95 математическое ожидание α нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интервала.

Отв. -0,04 < α < 0,88.

 

10. По данным 9 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений 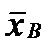= 30,1 и исправленное среднее квадратическое отклонение s = 6. Оценить истинное значение измеряемой величины с помощью доверительного интервала с надежностью γ =0,99.

Отв.. 23,38 < α < 36,82

 

11. По данным 16 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений 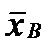= 42,8 и исправленное среднее квадратическое отклонение s = 8. Оценить истинное значение измеряемой величины с надежностью γ = 0,999.

Отв. 34,56 < α < 50,94.

 


1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)